


Notions fondamentales d’acoustique
Article disponible au format pdf
- Courbes de Fletcher et Munson
____________________________________________________________________
Un son est une sensation auditive engendrée par une onde acoustique. Cette onde est générée par une vibration (cordes vibrantes, cordes vocales, membrane d’un haut- parleur,…). Vibration qui va créer un déplacement de particules du milieu de propagation (air, eau,…) autour d’une position d’équilibre.
Le son ne se propage donc pas dans le vide.
La différence entre un son et un bruit est assez vague et cette appréciation est différente selon chacun. Un son est défini en tant que bruit lorsque celui- ci est désagréable, gênant. Dans la vie de tous les jours, nous avons tendance à juger différemment le bruit que nous faisons de celui que nous subissons. Le meilleur exemple reste l’aspirateur passé par un de vos proches ou la musique que vous détestez écoutée par votre ami ou amie.
La vitesse du son (ou célérité C) va dépendre de la densité du milieu de propagation et de la température.
La vitesse de propagation du son dans l’air à 20° C est de 340 m/s (mètres par seconde), de 1480 m/s dans une eau à 20° C et de 6000 m/s dans l’acier.
Plus le milieu est dense, plus la vitesse de propagation du son sera importante.
La température va également jouer un rôle : Plus le milieu est chaud, plus l’agitation des molécules qui le compose augmente et favorise la transmission. A l’inverse, dans un milieu froid la vitesse du son diminue. A 0° C, la vitesse des ondes sonore est de 331 m/s dans l’air.
Le son peut être caractérisé par trois paramètres :
- La fréquence (ou sa hauteur)
- L’intensité (ou le niveau sonore)
- Le timbre (la « richesse » du son)
La fréquence est le nombre d’oscillations périodiques par seconde. Elle s’exprime en Hertz (Hz). On parlera également de hauteur d’un son.
Une fréquence de 100 Hz correspondra donc à 100 oscillations par seconde.
La fréquence est l’inverse de la période.
F= 1/T
F = fréquence en Hz
T= période
Fréquence de 2 Hz
Relations entre fréquence, période et longueur d’onde
Fréquence 100 Hz 1000 Hz 10 000 Hz
Période T=1/f 10 ms 1 ms 0,1 ms
Longueur d’onde λ = C/F 3,4 m 0,34 m 0,03 m
Plus un son sera aigu et plus sa fréquence sera haute. A l’inverse, plus un son sera grave, plus sa fréquence sera basse.
Les fréquences audibles par l’être humain s’étendent de 20 à 20 000 (20 K) Hz. Ces chiffres peuvent varier suivant l’âge et les personnes.
Notons également que nos oreilles sont plus sensibles aux fréquences médium et aigues, correspondant aux fréquences de la voix.
En dessous de 20 Hz, il s’agit d’infrasons et d’ultrasons au dessus de 20 KHz. Ceux- ci ne donnent pas lieu à une sensation sonore.
Les courbes dites de Fletcher & Munson, du nom des deux scientifiques qui les ont établies à l’aide de mesures effectuées sur un large panel d’individus, illustrent le fait que la sensibilité de l’oreille n’est pas identique à toutes les fréquences. Ces courbes, aussi appelées « isosoniques », représentant la sensibilité moyenne de l’oreille pour une plage de fréquences audibles.
Ces courbes sont paramétrées en phones. Par définition, le numéro de chaque courbe (ou niveau en phones) est égal à l’intensité correspondant en décibels à une fréquence de 1000 Hz.
Ces courbes indiquent, pour chacune des fréquences du spectre audible, le niveau de pression acoustique (SPL pour Sound Pressure Level) nécessaire à la perception d’une même intensité, d’où le terme « courbe d’égale (iso) sensation sonore (sonique) ».
Prenons un exemple : si vous prenez comme référence un signal à 1 KHz émis à un niveau de 60 dB, et que vous le comparez à un signal de 40 Hz, ce dernier devra être d’un niveau non plus de 60 dB mais de 80 dB pour que vous ayez une sensation sonore identique. Si vous comparez ensuite ce même signal à 1 KHz avec un autre à 8 KHz, ce dernier devra être émis à un niveau de 70 dB pour que vous ayez une sensation sonore identique pour les deux signaux.
D’une manière générale, l’oreille est moins sensible aux fréquences graves et aiguës qu’aux fréquences médiums, comprises entre 1 KHz et 5 KHz, qui sont naturellement favorisées par notre oreille.
Applications :
Loudness : Le correcteur loudness présent sur quelques amplificateurs Hifi permet à bas niveau d’amplifier les fréquences graves et aiguës afin d’obtenir la sensation d’un son équilibré en niveau sur toute la bande de fréquences audibles.
dB(A), dB(B), dB(C) : Afin de faire correspondre aux mieux les mesures, des courbes de pondérations ont été créées. Ces pondérations vont permettre de tenir compte approximativement de la variation de la sensibilité de l’oreille en fonction de la fréquence et de l’intensité.
- Pondération A dB(A) : pour des niveaux de 25 à 55 dB
- Pondération B dB(B) : pour des niveaux de 55 à 85 dB
- Pondération C dB(C) : pour des niveaux supérieurs à 85 dB
La longueur d’onde est la distance parcourue par une onde acoustique pendant une période.
Elle se calcule comme suit :
λ = C/F
Avec λ (Lambda) en mètres
C (célérité) en m/s (340 m/s pour l’air)
F la fréquence en Hertz
Fréquence Longueur d’onde
20 Hz => 17 m
100 Hz => 3.4 m
500 Hz => 0.68 m
1000 Hz => 0.34 m
5000 Hz=> 0.07 m
10 000 Hz=> 0.03 m
20 000 Hz=> 0.02 m
On peut remarquer que plus la fréquence augmente, plus la longueur d’onde diminue.
La courbe de réponse en fréquence (ou bande passante) correspond à la représentation graphique des diverses fréquences en fonction de leur niveau.
Cette courbe indique donc la plage de fréquences que l'enceinte, le micro, l’enregistreur,… est capable de restituer ou de reproduire.
L'idéal théorique en analyse logarithmique se traduit par une courbe horizontale linéaire, permettant une reproduction ou une restitution de toutes les fréquences avec la même intensité. En pratique, il n’en est pas de même.
La courbe de réponse en fréquence est généralement donnée dans un gabarit de +/- 3 dB par rapport à un niveau de référence (généralement 0 dB à 1000 Hz). On peut alors observer sur le graphique de la courbe de réponse en fréquence les différences de niveaux pour chaque fréquence.
Il arrive également souvent que seule la réponse en fréquence (ou bande passante) soit donnée dans les fiches techniques. Il n’y aura alors pas de graphique pour l’illustrer.
On donnera par exemple comme indication : 60 à 18 000 Hz à +/- 3 dB.
…La1 La2 La3 La4 La5 ...
…110 Hz220Hz440Hz880Hz1760Hz…
Doubler la fréquence revient à monter d’une octave. Diviser la fréquence par deux revient à descendre d’une octave.
Il y aura donc deux octaves entre le La1 (110 Hz) et le La3 (440 Hz).
Cette notion d’octave est très souvent utilisée et principalement le tiers d’octave, notamment dans l’utilisation de filtres tels que les équaliseurs,…
Equaliseur tiers d’octave BSS FCS-960
Les fréquences en tiers d’octave sont alors :
20 - 25 – 31 – 40 - 50 – 63 - 80
100 – 125 – 160 - 200 - 250 – 315 – 400 – 500 – 630 – 800
1000 – 1250 – 1600 – 2000 – 2500 – 3150 – 4000 – 5000 – 6300 – 8000
10 000 – 12 500 – 16 000 - 20 000
Une source sonore telle une sphère pulsante émet une puissance acoustique (exprimée en watts) dans toutes les directions. Plus on s’éloigne du centre de la sphère, plus la puissance par unité de surface (l’intensité) va diminuer.
Pour une source sphérique, la conséquence est que le niveau sonore va décroître de 6 dB lorsqu’on double la distance.
L’intensité est donc la puissance par unité de surface.
L’intensité acoustique la plus faible perceptible par l’oreille humaine est de l’ordre de 10-12 W/m² (1/ 1 000 000 000 000 W/ m²). Le seuil de douleur est lui fixé à 1 W/m².
Le rapport entre ces deux valeurs est donc de 1 à mille milliards.
Cette échelle n’étant pas la plus pratique à utiliser, c’est le Bel qui a été choisi comme unité de référence. Et afin de mieux détailler l’échelle sonore, c’est le décibel (dB) (soit un dixième de Bel) qui a été finalement été utilisé.
Niveau sonore = 10 log (I / 10-12)
I = Intensité acoustique à mesurer
Intensité acoustique (W/m²) Niveau (bel) Niveau (dB)
1 =>12 =>120
10-2 10 100
10-4 8 80
10-6 6 60
10-8 4 40
10-10 2 20
10-12 0 0
En résumé, l’intensité d’un son correspond à son niveau sonore, niveau exprimé en décibels (unité que l’on doit à Alexander Graham Bell (1847-1922)).
Le seuil d’audition de notre oreille se situe à 0 dB, le seuil de douleur aux alentours de 120 dB.
Echelle de bruit
Sans danger pour l’audition :
0 dB Seuil d’audition
15 dB Bruissement de feuilles
20 dB Chuchotement / Jardin paisible
25 dB Conversation à voix basse
30 dB Appartement dans un quartier tranquille
35 dB Bateau à voile / Tic tac de montre
40 dB Rue résidentielle
50 dB Bruit d’une voiture au ralenti
60 dB Grands magasins / Sonnerie de téléphone
70 dB Restaurant bruyant
85 dB Radio volume à fond / Tondeuse à gazon
Facteur de troubles auditifs :
90 dB Rue au trafic intense
95 dB Atelier de forgeage / Train passant en gare
Pénible à entendre :
100 dB Marteau piqueur / Baladeur à fond
105 dB Discothèque / Concert
Difficile à supporter :
110 dB Atelier de chaudronnerie
Seuil de la douleur :
120 dB Moteur d’avion
130 dB Décollage d’un avion / Formule 1
Exige une protection auditive :
140 dB Turbo réacteur au banc d’essai
180 dB Fusée Ariane au décollage
L’addition des décibels ne se fait pas de manière arithmétique mais selon une progression logarithmique. Deux sources d’un niveau sonore de 70 dB chacune ne donneront pas au final une source sonore équivalente de 140 dB mais bien de 73 dB. En effet, doubler la source sonore revient à ajouter 3 dB.
Pour une sensation doublée du niveau sonore, il faudra ajouter 10 dB. Ce qui revient à multiplier par 10 la source.
Augmentation du niveau sonore en dB Changement dans la perception auditive
3 dB: A peine perceptible
5 dB: Différence audible
10 dB: Sensation doublée
15 dB: Large différence
20 dB: Sensation quadruplée
Cependant, l’acoustique ne se limite pas à une mesure “physique” des sons. Le son est pour l’oreille humaine à la fois une notion objective et subjective. L’oreille n’a pas la même sensibilité pour toutes les fréquences audibles. En effet, un son de 50 dB et de fréquence 1000 Hz produit une sensation auditive plus forte qu’un son de 50 dB à la fréquence 100 Hz. Pour tenir compte de cette particularité de l’oreille humaine, la mesure de la “force sonore”, au sens physiologique, utilise des filtres qui pondèrent les niveaux sonores en fonction des fréquences. La mesure est alors exprimée en décibel A ou dB (A).
Le timbre d’un instrument correspond à sa richesse sonore. Une même note jouée sur deux instruments différents ne donnera pas au final le même son.
Chaque son est formé d’une fréquence fondamentale et de fréquences harmoniques”. On dit qu’un son est riche, agréable à entendre, lorsqu’il contient de nombreuses harmoniques. Un son pauvre en harmoniques paraîtra terne à notre oreille. Un son ne comprenant qu’une seule fréquence est appelé “son pur” (extrêmement rare dans notre environnement quotidien). Les sons musicaux sont des “sons complexes”, mélanges de sons graves et aigus. Le son musical est la superposition d’un son fondamental et d’harmoniques dont les fréquences sont des multiples de la fréquence fondamentale.
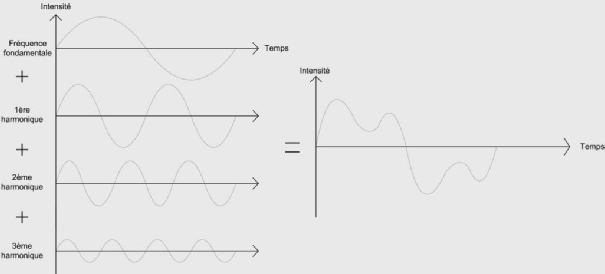
C’est donc la richesse en harmonique d’un instrument qui détermine le timbre d’un instrument.
_________________
Didier Pietquin 2008©
Sources: Images issues des articles de la firme Bruël & Kjaer ainsi que du livret pédagogique: "Les risques auditifs" publié par le RIF
Influence du taux d’humidité (hygrométrie) sur la propagation sonore:
Le degré d’hygrométrie influencera la propagation sonore et principalement l’atténuation des hautes fréquences.
Pour rappel, le degré d’hygrométrie correspond au taux d’humidité dans l’air. En effet, plus le degré d’hygrométrie sera faible (plus l’air est sec), plus les aigus seront atténués.
Ce qui signifie que plus l’air sera sec (et donc un taux d’humidité faible), plus l’atténuation des aigus sera importante.

| Moteur de recherche |
| Plan du site |
| Blog |
| Son |
| Eclairage |
| Electricité |
| Câblage et connectique |
| Bien débuter |
| Acoustique |
| Line Array - Ligne source |
| Impédance - HP |
| Décibels |
| DI Box |
| Adaptation d'impédance |
| Symétrique - Asymétrique |
| Lignes 100 volts |
| Consoles |
| Acoustique fondamentale |
| Timbre |
| Phase: Première partie |
| Directivité des basses fréquences |
| End fire |
| End Fire 2 |
| Sources sonores - propagation |
| WST |
| Circuits auxiliaires |
| INSERTS |
| Groupes |
| Bouchon DMX |
| Câbles multipaires électriques |
| Electricité - Notions élémentaires |
| Tableaux électriques |
| L'électricité pour nos spectacles |
| Multimètres - Utilisation |
| Indices de protection (IP) |
| Branchements |
| Relier les enceintes |
| Les types de câbles |
| Câbles électriques |
| Réaliser ses adaptateurs |
| Connecter un clavier |
| Série et parallèle |