


Article disponible au format pdf
(Mise à jour: Mai 2007)
En vue de compléter les explications sur la technologie des systèmes dits « Lignes sources », voici un second article reprenant quelques notions théoriques. Celui- ci est largement inspiré de ce qu’à écrit Alain Pouillon – Guibert dans le magazine Sonomag de novembre 2003.
Certaines notions qui m’ont semblées intéressantes ont été ajoutées ou légèrement approfondies. De même que certains aspects ne l’ont pas étés.
Cet article n’a bien sûr pas pour but de remplacer des ouvrages scientifiques écrits par des ingénieurs mais bien d’essayer de rendre le plus abordable possible quelques notions qui peuvent paraître abstraites.
1. Quelques notions d’ acoustique
Qu’est-ce qu’un son ? Comment est-il produit ?
La production d’un son est due à des vibrations mécaniques. Vibrations produites par nos cordes vocales, la membrane d’un haut- parleur, les cordes d’une guitare,… Les molécules d’air (ou du milieu de propagation en général) vont osciller autour d’une position d’équilibre.
Les molécules ne vont donc pas se déplacer.
Le son n’est donc pas un transport de matière mais d’énergie.
Pour mieux visualiser la propagation du son, je vous invite à visiter la page de Dan Russel (http://www.kettering.edu/~drussell/demos.html)
Pour visualiser la propagation sonore, l’exemple universel est la pierre que l’on jette à la surface d’eau calme.

Si on place un bouchon sur la surface de l’eau, celui- ci ne s’éloignera pas. Il se contentera d’osciller de bas en haut.
Avant d’entrer dans le vif du sujet, voyons quelques notions intéressantes ou dont nous ferons usage par la suite.
Un front d’onde est une surface virtuelle formée par l’ensemble des points qui vibrent en phase.
En reprenant notre caillou jeté dans l’eau, on peut observer des cercles concentriques dont le centre est le point d’impact du caillou avec l’eau.
Tous les « points » d’un même cercle oscillent simultanément. Voilà ce qu’est notre front d’onde.
Dans l’air, les fronts d’ondes ne seront plus des cercles concentriques mais des sphères, le son se propageant dans trois dimensions.
Un front d’onde sera donc une sphère dont tous les points sont situés à une même distance de la source et qui vibrent donc en phase.
Plus on s’éloigne du centre d’une sphère, plus la courbure de celle- ci semble faible.
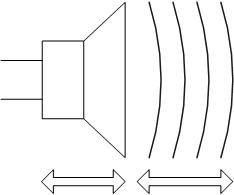
Pour une source sonore, c’est le même principe. A proximité du point source, les ondes sont sphériques. Plus on s’ éloigne, plus les ondes seront considérées comme planes. L' approximation veut qu' on parlera d’ ondes planes. Cependant, la propagation reste sphérique.

Sa célérité ou vitesse de propagation
La vitesse du son (sa célérité) va dépendre de la densité du milieu de propagation et de la température.
Plus le milieu sera dense et plus le son se propagera vite, de même que plus la température sera élevée et plus le son se propagera vite.
A une température de 0°C, la vitesse du son dans l’ air est de 330 m/s (mètres par seconde).
A 20°C, la vitesse du son dans l’air est de 340 m/s. C’ est cette valeur qui est la plus utilisée pour les calculs.
Fréquence
La fréquence correspond au nombre d ’oscillations périodiques par unité de temps.
La période est le temps que met une onde sonore pour accomplir un cycle complet. On la note T et est mesurée en seconde.

La fréquence est l’inverse de la période.
F = 1/T
Longueur d’onde
La longueur d’onde (notée lambda λ) est la distance parcourue par une onde pendant une période.
Cette distance est calculée en mètre.
λ = C/F
C correspondant à la célérité (340 m/s à 20°C)
F correspondant à la fréquence en Hertz
Onde transversale et longitudinale
Une onde est transversale lorsque les particules oscillent dans une direction perpendiculaire à la direction de propagation de l’onde.
C’est le cas de notre caillou jeté dans l’eau.
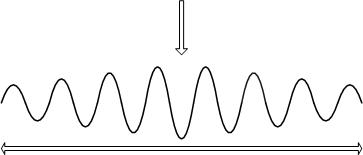
Une onde est longitudinale lorsque les particules vibrent dans la même direction que la propagation de l’onde. C’est le cas des ondes sonores.
3. Caractéristiques énergétiques
Onde circulaire
Lorsqu’on observe notre eau troublée par le jet du caillou, on remarque que plus on s’éloigne du centre et plus les cercles voient leur amplitude diminuer. Plus simplement, on peut remarquer que la hauteur des « vagues » diminue lorsqu’on s’éloigne du centre.
Comment cela se passe-t-il ?
Il est assez facile de constater que le rayon de nos cercles (ou vagues) augmente petit à petit. On peut aussi déclarer que l’énergie reste constante pour chaque cercle et que celle- ci s’étale donc au fur et à mesure de la grandeur des cercles.
L’énergie devient donc négligeable lorsque le rayon devient très grand.

Utilisons les mathématiques pour illustrer nos propos.
Prenons deux cercles concentriques dont le centre est notre point source. L’énergie est constante sur chacun de ces cercles dont on connait le périmètre (2πR). Appelons cette énergie E. Prenons un point P sur chaque cercle.
On peut donc calculer la quantité d’énergie par unité de longueur.
Ep = E/2πR
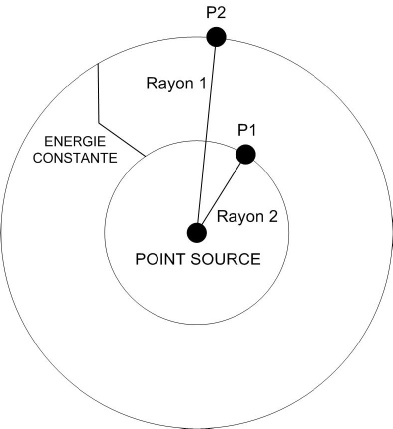
Exemple chiffré :
Considérons que l’énergie totale E est égale à 1000 (peu importe l’unité).
Considérons le premier cercle dont le rayon est de 10 cm et dont nous noterons un point P1.
Considérons le deuxième cercle dont le rayon est de 20 cm et dont nous noterons un point P2.
Périmètre du cercle 1 : 2π10 soit 62,8 cm
Périmètre du cercle 2 : 2π20 soit 125,6 cm
L’énergie au point P1 est donc de 1000/ 62,8 soit 15,92
L’énergie au point P2 est donc de 1000/ 125,6 soit 7,96
On remarque par cet exemple chiffré que l’énergie décroît, pour un point donné, proportionnellement en fonction de l’éloignement de la source. On remarque aussi que l’énergie a diminué de moitié alors que la distance a doublé.
En parlant de façon plus « scientifique », on peut exprimer la variation d’énergie d’une distance R1 à une distance R2 par la formule suivante 10 log R2/R1.
L’unité utilisée sera le décibel, décibel exprimant le rapport entre deux grandeurs.
Pour exprimer le rapport de l’énergie lors d’un doublement de la distance dans le cas d’une onde circulaire, cela donnera : 10 log 2 soit 3 dB.
Onde sphérique
Nous avons vu au début de cet article que le son ne peut pas être assimilé à une onde circulaire mais bien à une onde sphérique, celui- ci se propageant en effet dans les trois directions de l’espace qui nous entoure.
L’exemple pris par Alain Pouillon- Guibert est celui d’un ballon dont le volume varierait au rythme de la musique.
Ici aussi, on peut constater que l’énergie totale reste conservée du passage d’une sphère à une autre. Les sphères distantes d’une distance R du point source étant l’image exacte de celui- ci.
Réutilisons les mathématiques pour illustrer nos propos.
Prenons deux sphères concentriques dont le centre est notre point source. L’énergie est constante sur chacune de ces sphères dont on connait la surface (S= 4πR²). Appelons cette énergie E. Prenons un point P sur chaque sphère.
On peut donc calculer la quantité d’énergie par unité de surface.
Ep = E/ 4πR²

Exemple chiffré :
Considérons que l’énergie totale est égale à 10 000.
Considérons la première sphère dont le rayon est de 10 cm et dont nous noterons un point P1.
Considérons la deuxième sphère dont le rayon est de 20 cm et dont nous noterons un point P2.
Surface de la sphère 1 : 4π10² soit 1256 cm²
Surface de la sphère 2 : 4π20² soit 5024 cm²
L’énergie au point P1 est donc de 10 000/ 1256 soit 7,96
L’énergie au point P2 est donc de 10 000/ 5024 soit 1,99
On remarque que par cet exemple chiffré, l’énergie décroît, proportionnellement au carré de la distance du point source à un autre point P.
En parlant de façon plus « scientifique », on peut exprimer la variation d’énergie d’une distance R1 à une distance R2 par la formule suivante 10 log R2²/R1² ou plus simplement par 20 log R2/R1.
L’unité utilisée sera le décibel, décibel exprimant le rapport entre deux grandeurs.
Pour exprimer le rapport de l’énergie lors d’un doublement de la distance dans le cas d’une onde sphérique, cela donnera 20 log 2 soit 6 dB.
Application aux enceintes acoustiques
Et nous voilà au point le plus important. Nous venons juste de voir que la pression sonore va décroître de 6 dB lorsque la distance est doublée avec une source sphérique, c’est-à-dire nos enceintes classiques.
Voici un tableau illustrant les pertes en fonction de l’éloignement à la source, sachant que le niveau sonore servant de base est en général celui prit à 1 mètre de la source sonore.
Distances, par rapport à la source Pertes
Cette perte en énergie sera un réel problème lorsqu’il s’agira de couvrir des zones importantes en extérieur par exemple. C’est ce que nous décrivons dans le paragraphe « Choix du système de diffusion » dans la deuxième partie de cet article consacrée aux critères de la WST.
En plus de ce problème d’atténuation, nous verrons plus loin l’importance de la directivité.
4. Une solution ?
Même si nous avons déclaré qu’une source sonore s’apparente à une source sphérique ou omnidirectionnelle (qui se propage dans toutes les directions), ce n’est pas tout à fait le cas.
On peut en effet dire qu’une source est omnidirectionnelle si ses dimensions sont petites par rapport à la longueur d’onde du son émis.
Une source sera donc d’autant plus omnidirectionnelle que la fréquence émise est basse.
En effet, plus les longueurs d’onde seront grandes et plus la membrane d’un haut-parleur apparaîtra comme un point. C’est le même principe lorsque vous êtes loin de quelqu’un, celui- ci vous semble tout petit.
L’onde sera alors sphérique, celle- ci se propageant dans toutes les directions.
Par contre, pour les hautes fréquences, et donc les courtes longueurs d’onde, notre membrane très grande se comporte plutôt comme un piston. La propagation étant alors plus directive.
On peut aussi établir une autre comparaison simple entre la taille de la membrane et la longueur d’onde.
Pour une fréquence de 100 Hz, la longueur d’onde est de 3,4 mètres. Cela correspond plus ou moins à un rapport de 10 si l’on prend une membrane de 38 cm de diamètre comme référence.
Pour une fréquence de 10 KHz (longueur d’onde 3,4 cm), le rapport s’approchera en général de 1, la taille des tweeters étant nettement inférieure à celle des woofers.
Source ponctuelle
On parlera de source ponctuelle pour une source idéale, correspondant au modèle de notre sphère. Dans la pratique, une source sera ponctuelle lorsque ses dimensions sont petites devant la longueur d’onde.
Avant d’aller plus loin, attardons- nous au rayonnement des sources acoustiques.
La directivité
Toute source sonore possède donc sa propre directivité, dépendante de la fréquence. Celle- ci pourra être mesurée en observant l’énergie perçue à un point P, distant de r du point source et variant suivant l’angle θ entre l’axe principal et la droite qui le relie au point P.
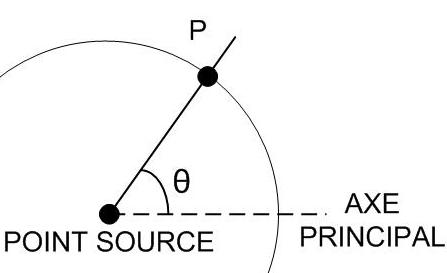
Diagramme de directivité
Grâce à ces mesures, on peut établir un diagramme de directivité représentant l’énergie perçue dans une certaine direction par rapport à l’axe principal du haut- parleur.
Il faudra reproduire ce diagramme pour chaque fréquence, celui- ci étant de plus en plus étroit au fur et à mesure que la fréquence augmente.
Un exemple vous est donné ci- dessous avec une enceinte Electro- Voice :
Pour des sources multiples (plusieurs haut- parleurs), on peut également remarquer l’apparition de différents lobes entre lesquels l’intensité est théoriquement nulle. Ces lobes seront d’autant plus nombreux que la fréquence augmente.
Ceci est dû au fait que même si tous les points sources émettent parfaitement en phase, un auditeur placé à une certaine distance des haut- parleurs ne les percevra pas en même temps. En effet, le trajet entre les différents haut- parleurs et l’auditeur ne seront pas identiques. Des interférences vont donc apparaître.
Dans certains cas, on peut justement décaler (ou re- caler) les différentes enceintes en modifiant la phase des sources sans les déplacer afin d’éviter ces phénomènes d’interférences.
En fonction de l’emplacement du récepteur (un micro par exemple), ces sources ponctuelles peuvent lui parvenir soit en phase soit en opposition de phase mais également toutes les nuances entre ces deux extrêmes.
Voici une page très intéressante illustrant ces phénomènes: http://www.kettering.edu/~drussell/Demos/superposition/superposition.html
Il y aura donc des endroits avec une atténuation de l’intensité (opposition de phase), d’autres avec une amplification lorsque les ondes seront en phase et tous les phénomènes possibles entre ces deux extrêmes.
Ceci se traduisant par des lobes de directivité, ceux- ci dépendant de la taille de la source, de l’emplacement de l’auditeur et bien sûr de la fréquence.
Pour une source omnidirectionnelle, elle le sera lorsque son intensité est constante quelque soit sa direction et quelque soit sa fréquence. Pour notre enceinte acoustique dont les diagrammes sont illustrés ci- dessus, ce n’est bien sûr pas le cas. Celle- ci sera d’autant plus directive que sa fréquence augmente.
Certains constructeurs vont présenterons la directivité de leurs enceintes selon un diagramme « Isobar », ou plus simplement, d’égale pression sonore. C’est le cas de D&B par exemple :
Sur l’axe des abscisses (X), vous retrouvez les fréquences. Sur l’axe des ordonnées (Y), vous retrouvez les valeurs pour les différents angles. 0 étant l’axe principal de l’enceinte.
La partie en gris clair indique une atténuation de 3 dB alors que celle en gris foncé indique une atténuation de 6 dB.
Il est utile de remarquer qu’avec un diagramme isobar, une enceinte dont la directivité est supérieure à 120° (une enceinte omnidirectionnelle par exemple) ne pourra être représentée.
Une enceinte à directivité constante sera elle représentée par une ligne droite.
Cas d’un haut- parleur
Bien que le mode sphérique corresponde à bons nombres de sources sonores, un haut- parleur agira différemment. Celui- ci se comportera en effet comme un piston.
Voyons maintenant comment se propagent les vibrations sonores produites par ce haut- parleur.
Deux zones de progression différentes peuvent être décrites. Ces deux zones sont appelées zone de Fresnel (zone de champ proche) et zone de Fraunhofer (zone de champ lointain).
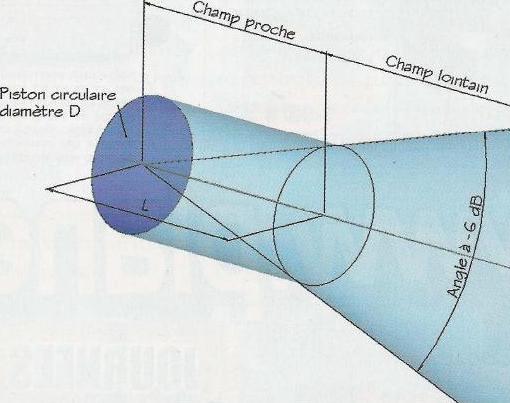
L’onde générée dans cette zone est une onde plane. Son intensité sonore est constante et ne varie pas en fonction de la distance.
Si le haut- parleur est très grand, l’onde qui y est produite est sensiblement plane tant que l’on se trouve à proximité de la membrane.

La zone A correspond à des ondes planes. La zone B à des ondes sphériques.
La partie C est une zone intermédiaire.
Ceci a cependant de très rapides limites.
(Nous reviendrons sur l’approche de Fresnel d’une manière différente dans un autre article.)
Après une courte distance, cette onde plane va se transformer en onde sphérique, selon un angle de 1,22 λ/ D = (sin θ/2). Le centre de celle- ci sera le centre de notre piston.
Pour calculer cette distance, appelée distance de transition et notée L, nous utiliserons la formule suivante :
L = D²/ 2λ
En remplaçant λ par C/F :
L = D² x F / 2 x C
Soit
L = D²F/ 680
Exemple chiffré :
Dans le cas d’un haut- parleur de 46 cm, dont la fréquence haute de coupure est située à 100 Hz :
0,46² x 100 / 680
Soit
21,16 / 680
Soit
31 mm !
Cette zone arrive donc très vite a ses limites.
Ce calcul est identique et peut- être appliqué à un piston carré.
Evolution de notre piston
Alain Pouillon- Guibert applique dans son article ces formules à un système son utilisé lors d’un concert de U2. Ce système composé de 72 enceintes S4 par côté revient plus ou moins à former un carré de 10 mètres de côté.
Sachant aussi que le couplage des 46 cm se fait proprement jusqu’à 250 Hz dans ce système, on obtient une onde plane de 10 mètres de côté jusqu’à L= 10²x250/680 soit environ 37 mètres.
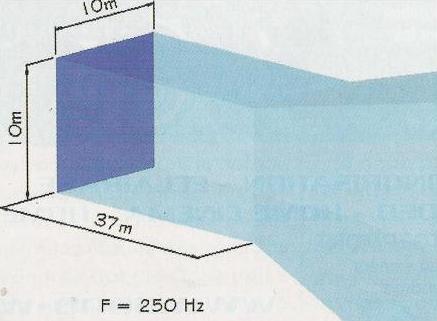
Ceci revient à dire que la zone de Fresnel s’étend sur une distance de 37 mètres, zone dans laquelle les auditeurs perçoivent la même intensité sonore quelque soit leur emplacement. Et ceci jusqu’à une fréquence de 250 Hz. Au-delà de cette fréquence, l’assemblage des enceintes S4 ne permet plus d’effectuer un couplage cohérent. Le calcul ne peut donc plus être utilisé.
Piston rectangulaire
Ce qui nous intéresse ici est évidemment la technologie des systèmes « Line Array ». Afin de nous en approcher tout doucement, déformons notre piston carré en forme rectangulaire.
Ceci nous amène à remarquer que les dispersions verticale et horizontale ne sont plus les mêmes, d’où l’apparition d’une zone intermédiaire dans laquelle l’onde ne propage pas de manière plane mais cylindrique.
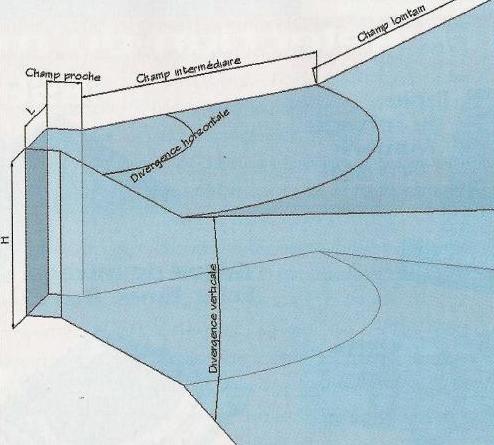
Après cette zone, l’onde est à nouveau sphérique.
Dans la zone intermédiaire qui nous occupe, l’intensité sonore va décroître proportionnellement par rapport à la distance qui sépare le point d’écoute à la source. La perte d’intensité n’est donc plus proportionnelle au carré de la distance et sera donc de 3 dB lors d’un doublement de la distance.
Et lorsque la distance est multipliée par 10, l’atténuation n’est plus que de 10 dB et non plus de 20 dB contrairement à une source sphérique.
Voilà qui devient intéressant !
La surface d’un cylindre est égale à 2πRH.
Le champ intermédiaire est donc un tronçon de cylindre de hauteur H et de rayon R. Soit R = H²F/680. Les valeurs limites à -6 dB sont données par l’angle de divergence horizontal du champ lointain soit 1,22 λ/L ou 1,22 λ/H.
Exemples chiffrés :
Prenons un ruban de 1 mètre de largeur et de 6 mètres de hauteur. Nous utiliserons 1000 Hz comme fréquence.
La profondeur du champ intermédiaire depuis la source en incluant le champ proche est la suivante :
R= 6² x 1000 / 680
Soit
36 000 / 680
Soit
52,94 mètres
L’angle d’ouverture est pour l’horizontal :
Sin (θ/2) = 1,22 λ/ L
Soit
1,22 x 340 / 1000 = 0,41 = Sin (θ/2)
Soit θ= 24,20° x 2 = 48,4°
L’angle d’ouverture est pour le vertical :
Sin (θ/2) = 1,22 λ/ H
Soit
1,22 x 340 / 6000 = 0,069 = Sin (θ/2)
Soit θ= 3,96° x 2 = 7,92°
En effectuant une diminution de la largeur de notre piston, celui- ci se comportera comme un cylindre de faible diamètre et son ouverture horizontale approchera les 360°.
Les champs proches et intermédiaires sont alors confondus et notre piston se comporte alors comme une ligne source.
Le problème qui se pose maintenant est que ce cylindre en ligne droite n’est pas spécialement adapté aux zones à sonoriser.
En gardant cette configuration, l’énergie sonore ne sera pas correctement répartie.
La solution va être de courber notre cylindre afin d’homogénéiser la couverture sonore, ceci impliquant également une ouverture verticale plus large.


En effectuant cette courbure, la propagation sonore s’approche d’un mode torique et non plus cylindrique.
De cette manière, l’onde sonore subit une décroissance intermédiaire entre l’onde cylindrique et l’onde sphérique.

En effet, plus le rayon du tore sera grand et plus il s’approchera d’un cylindre. Et inversement, plus son rayon sera petit et plus il s’approchera d’une sphère.

Nous voilà donc en présence de notre système Line Array, presque prêt à être installé. Ceci dit, pour qu’un système sonore corresponde à une ligne source, il faudra respecter plusieurs critères. Ceux- ci sont expliqués dans la partie WST.
En espérant que cette théorie puisse vous être utile, j’espère que la mise en pratique d’un tel système vous en sera facilitée.
Sources - Bibliographie
- Article « Rayonnement des sources linéaires continues » par Alain Pouillon- Guibert paru dans le SonoMag 285 de novembre 2003.
- Le livre des techniques du son (tome 2), sous la direction de Denis Mercier, Editions Dunod, 2004
- Acoustique des salles et sonorisation, J. Jouhaneau, Editions Tec & Doc, 2003
- Initiation à l’acoustique, A. Fischetti, Editions Belin, 2003
- Avec l’aimable autorisation d’Alain Pouillon-Guibert pour l’utilisation des schémas parus dans le magazine Sonomag
Didier Pietquin © Août 2006 (Mise à jour Mai 2007)




| Moteur de recherche |
| Plan du site |
| Blog |
| Son |
| Eclairage |
| Electricité |
| Câblage et connectique |
| Bien débuter |
| Acoustique |
| Line Array - Ligne source |
| Impédance - HP |
| Décibels |
| DI Box |
| Adaptation d'impédance |
| Symétrique - Asymétrique |
| Lignes 100 volts |
| Consoles |
| Acoustique fondamentale |
| Timbre |
| Phase: Première partie |
| Directivité des basses fréquences |
| End fire |
| End Fire 2 |
| Sources sonores - propagation |
| WST |
| Circuits auxiliaires |
| INSERTS |
| Groupes |
| Bouchon DMX |
| Câbles multipaires électriques |
| Electricité - Notions élémentaires |
| Tableaux électriques |
| L'électricité pour nos spectacles |
| Multimètres - Utilisation |
| Indices de protection (IP) |
| Branchements |
| Relier les enceintes |
| Les types de câbles |
| Câbles électriques |
| Réaliser ses adaptateurs |
| Connecter un clavier |
| Série et parallèle |