


La notion de phase est généralement une notion assez abstraite et difficile à comprendre. C’est pourquoi nous allons nous attarder à expliquer cela en détail dans cet article.
Voici un rapide aperçu de cet article :
1. Rappel de notions essentielles : fréquence, période et longueur d’onde
2. Le signal de départ : une sinusoïde
3. Addition de deux sinusoïdes
4. Expression des valeurs en dB
5. Graphique de réponse en phase
6. Exemples et visualisations via SmaartLive
Mais avant d’aller plus loin, reprenons quelques notions théoriques qui nous serons utiles : Fréquence, période et longueur d’onde.
La fréquence est le nombre d’oscillations périodiques par seconde. Elle s’exprime en Hertz (Hz). On parlera également de hauteur d’un son.
Les fréquences qui nous intéressent en audio varient de 20 Hz à 20 KHz.
Une fréquence de 100 Hz correspondra donc à 100 oscillations par seconde.
La fréquence est l’inverse de la période.
F= 1/T
F = fréquence en Hz
T= période
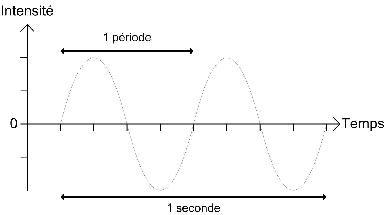
La longueur d’onde est la distance parcourue par une onde acoustique pendant une période.
Elle se calcule comme suit :
λ = C/F
Avec λ (Lambda) en mètres
C (célérité) en m/s (340 m/s pour l’air à 20°C, valeur utilisée pour nos calculs)
F la fréquence en Hertz
On peut donc établir le tableau suivant, mettant en relation fréquence, période et longueur d’onde.

La représentation d’un son pur (une fréquence unique) est donc une onde sinusoïdale. Sinusoïde qui est en relation directe avec le cercle trigonométrique.
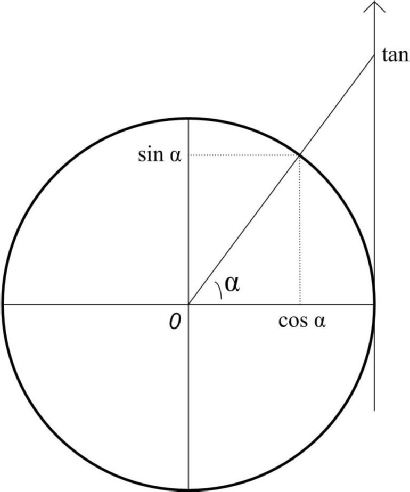
Voici la correspondance :
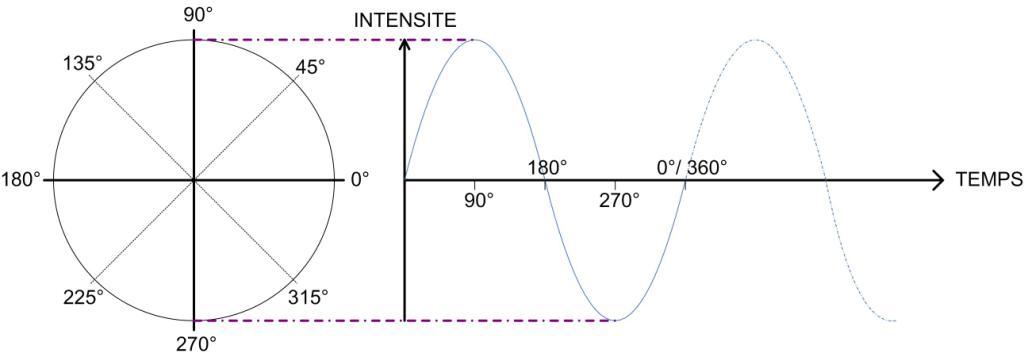
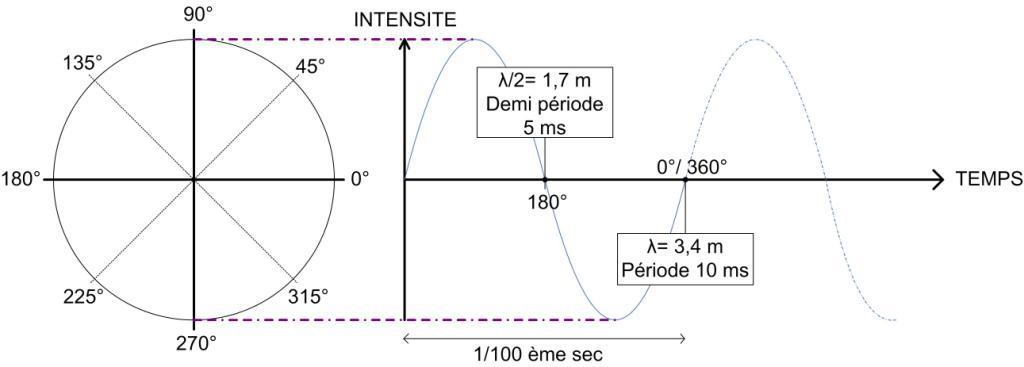
La phase
La phase est donc en rapport direct avec les notions de fréquence et longueurs d’onde.
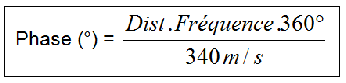
Avec la distance en mètre et la fréquence en Hertz.
Ci-dessous, une fréquence de 100Hz.
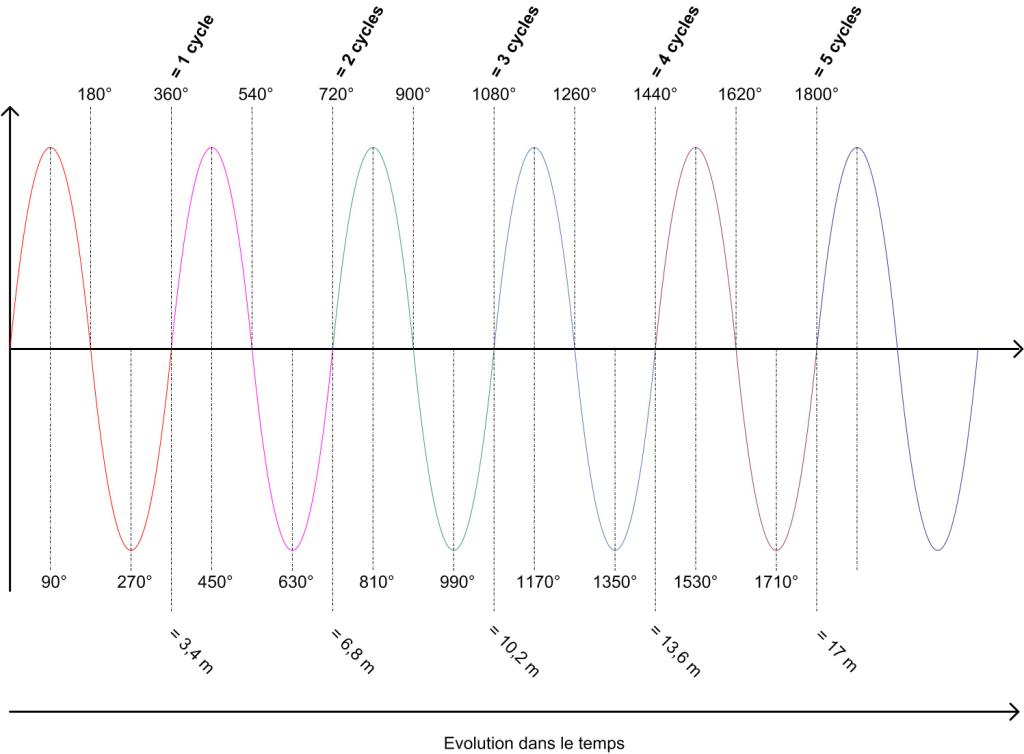
180° = 1.7m x 100Hz x 360º / 340m/s
360° = 3.4m x 100Hz x 360º / 340m/s
540° = 5.1m x 100Hz x 360º / 340m/s
720° = 6.8m x 100Hz x 360º / 340m/s
…..
Sur le graphique ci- dessus, on peut observer que l’évolution dans le temps de notre signal correspond à une évolution en degrés. Un cycle complet correspond à 360°. Un cycle plus tard, nous sommes à 720°. Et ainsi de suite…
Comme nous l’avons vu plus haut, il est facile d’établir la relation entre un cycle de 360° et une période. Période exprimée en milli- seconde (ms) et qui sera différente pour chaque fréquence. On peut donc par exemple dire qu’une fréquence de 100 Hz décalée d’un cycle (de 360°) par rapport à une autre de même fréquence sera retardée d’une période, soit 10 MS.
3. Addition de deux sinusoïdes :
Regardons maintenant ce qu’il se passe lorsque deux ondes de même fréquence, de même intensité mais de phases différentes sont additionnées.
Nous verrons au point suivant comment exprimer le résultat de cette addition, suivant que l’on se base sur une tension, une intensité ou une puissance.
L’expression mathématique est alors la suivante :
La valeur de l’onde résultante est égale à
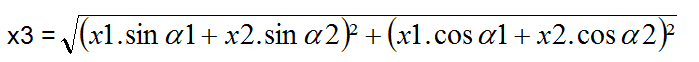
Ou x1 correspond à l’intensité de la première onde,
x2 à l’intensité de la deuxième onde,
x3 à la valeur résultante
α1 au déphasage de la première onde en degrés. (0° dans nos exemples)
α2 au déphasage de la deuxième onde, en degrés.
Appliquons maintenant cette formule à quelques exemples :
Deux ondes de même intensité et de même fréquence parfaitement en phase.
Le déphasage est de 0°. Les deux ondes débutent à l’origine.
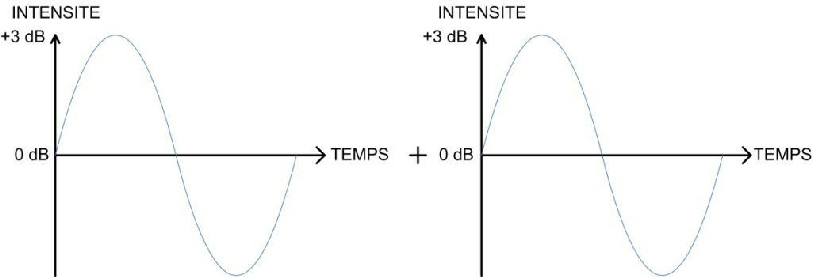
En prenant 1 comme valeur maximale de l’onde, la formule devient celle- ci :
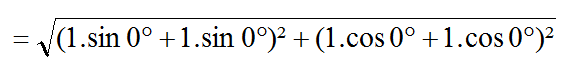
Sin 0° étant égal à 0 et cos 0° étant égal à 1, on peut simplifier la formule et la réduire à
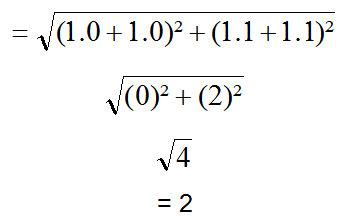
Dans ce cas précis, lorsque les deux ondes sont parfaitement en phase, il en résulte le double de l’intensité. On gagne donc 3 dB par rapport à l’intensité initiale.
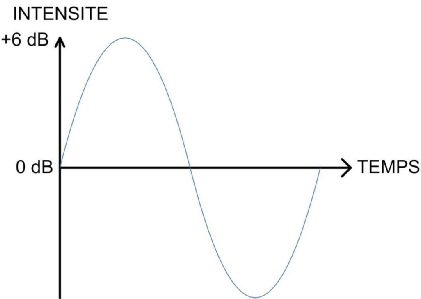
Mais lorsque l’une des deux sources est décalée de 90° par exemple, soit 2,5 ms ou encore d’un quart de la longueur d’onde (0,85 m) pour une fréquence de 100 Hz, le résultat est le suivant :
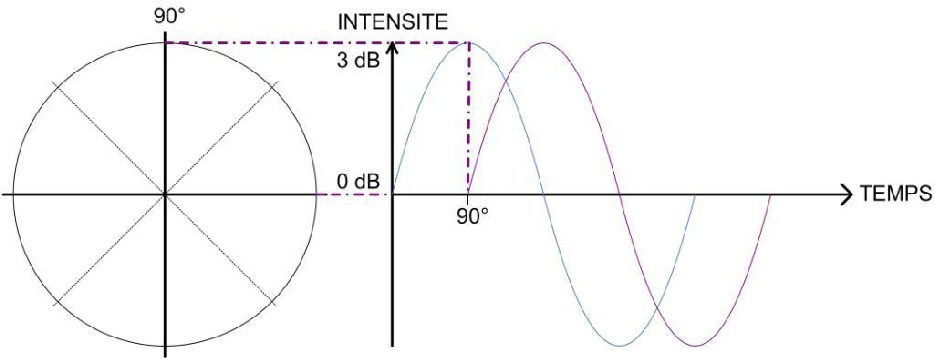
Toujours en gardant 1 comme valeur maximale de notre onde, la formule mathématique devient :

Le résultat de l’addition de deux sinusoïdes identiques dont l’une est déphasée de 90° correspond donc à 1,41 fois la valeur maximale d’une des deux sinusoïdes.
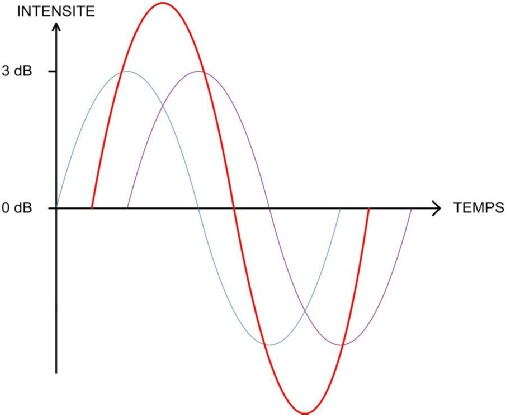
La sinusoïde résultante, en rouge, ne correspond plus au double de l’intensité mais à une intensité moindre.
Et lorsque le déphasage correspond à la demi-longueur d’onde (λ/2) ou à 180°, il en résulte ceci :
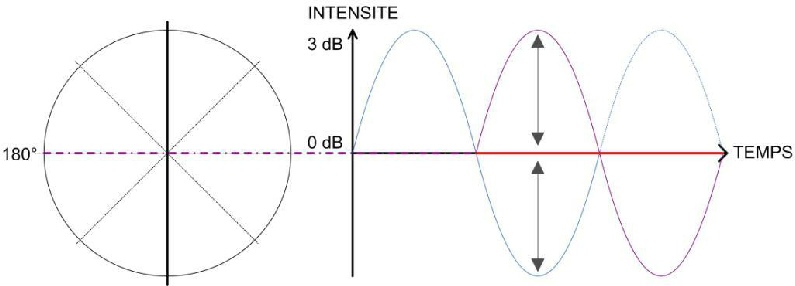
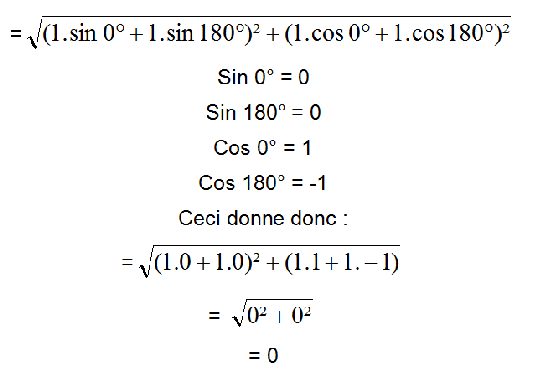
L’intensité résultante est donc nulle. Il y a donc une annulation pure et simple du signal puisque les deux sinusoïdes sont parfaitement opposées.
4. Expression de ces valeurs en dB
Nous venons de calculer l’intensité résultante de l’addition de deux sinusoïdes identiques en fonction du déphasage de l’une par rapport à l’autre.
Pour résumer, l’addition de deux ondes en phase correspond au double de l’intensité d’une sinusoïde.
Avec un déphasage de 90° d’une des deux ondes, la valeur résultante est de 1,41 fois.
Avec un déphasage de 180° d’une des deux ondes, la valeur résultante est nulle.
En effectuant le logarithme de cette valeur, il nous est aussi possible d’exprimer ces valeurs en décibels (dB).
Cependant, selon que l’unité d’origine est une tension, une intensité ou une puissance, le résultat sera différent.
En effet, lorsqu’on parle de tension, la valeur en décibel est égale à 20 log U2/U1
Par contre, lorsqu’on parle en intensité ou en puissance, la valeur en décibel est égale à 10. Log P2/P1 pour la puissance et 10.log I2/I1 pour l’intensité.
La formule que nous utiliserons pour la suite de cet article est la suivante :
=20.log x3
Les valeurs sont donc exprimées en décibel avec un gain positif ou négatif selon le déphasage.
Ce qui nous donne le tableau suivant :
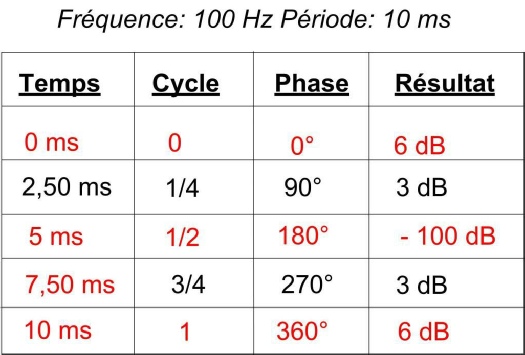
Ou encore sous cette forme :
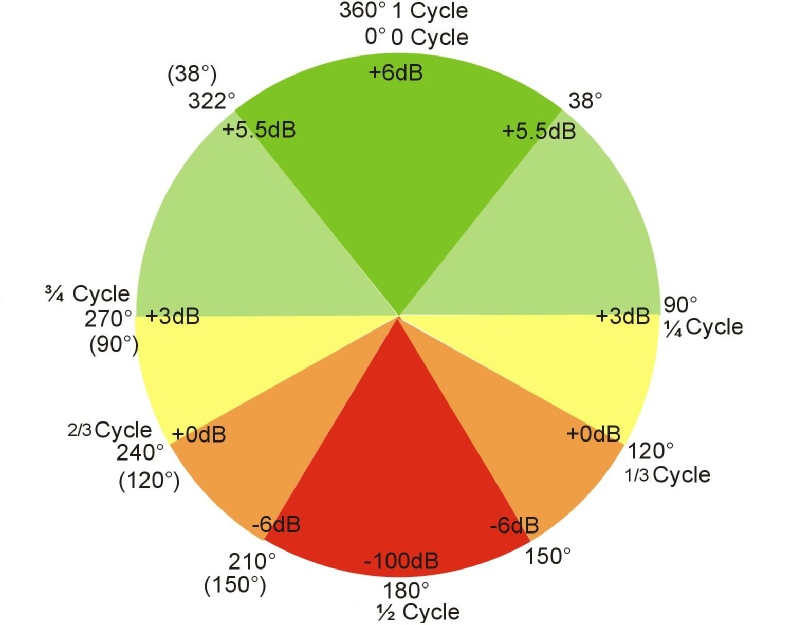
Explications :
Nous avons vu que lorsque deux sources sonores sont parfaitement en phase, l’intensité résultante est double. Nous obtenons un gain de 6 dB.
Reprenons notre fréquence de 100Hz. Lorsqu’une des deux sources est décalée par rapport à la première de 5 ms, cela correspond à un déphasage de 180°. L’intensité résultante est une annulation parfaite du signal.
Entre ces deux valeurs de déphasage, le graphique ci- dessus nous donne les différentes valeurs de l’intensité résultante.
5. Graphique de réponse en phase
En reprenant le graphique précédent et en « l’étirant », il va nous être possible de visualiser l’évolution de la phase dans le temps. Il devient donc un graphique en trois dimensions.
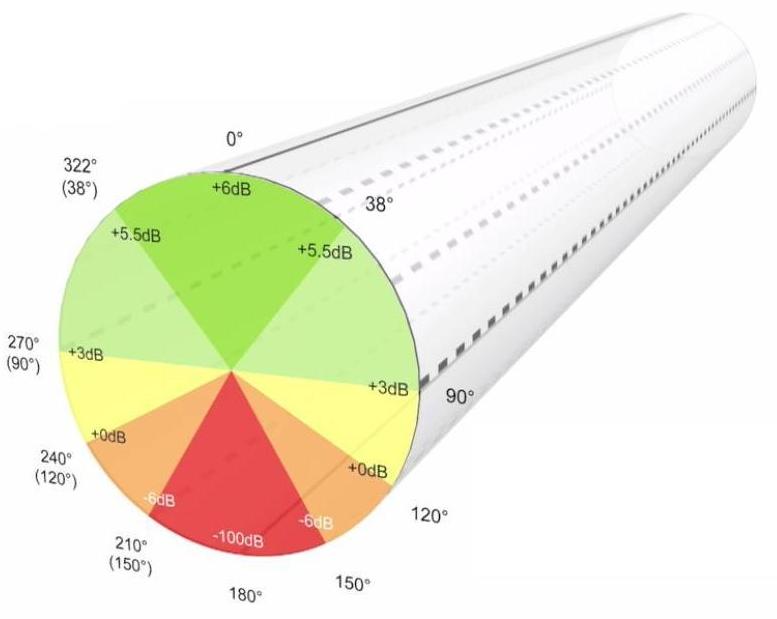
Par rapport à un signal de référence, appliquons un délai de 10 ms, ceci correspond à une rotation de 360° pour une fréquence de 100 Hz, lorsque ce délai est appliqué à toute la gamme du signal audio dont le niveau est égal et de même polarité à toutes les fréquences.
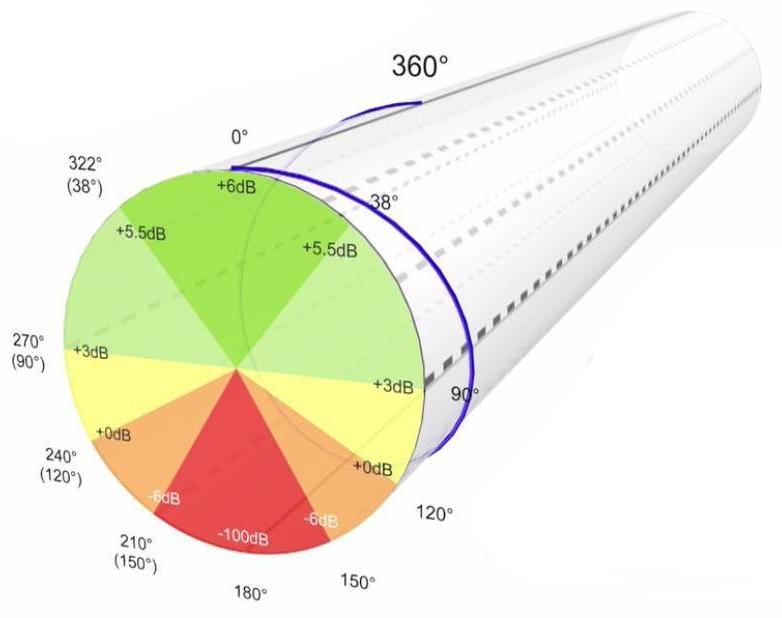
Ce même délai de 10 ms va provoquer une rotation de phase de 720° à la fréquence de 200 Hz.
En effet, la période d’une fréquence de 200 Hz est de 5 ms.
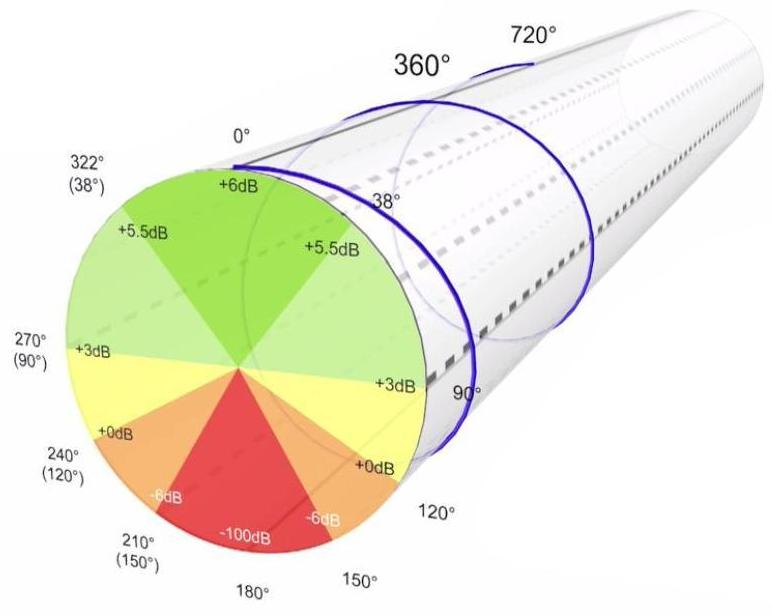
Et ainsi de suite… 10 ms correspondent à une rotation de phase de 1080° à une fréquence de 300 Hz. Puisque la période d’une fréquence de 300 Hz est de 3,3 ms.
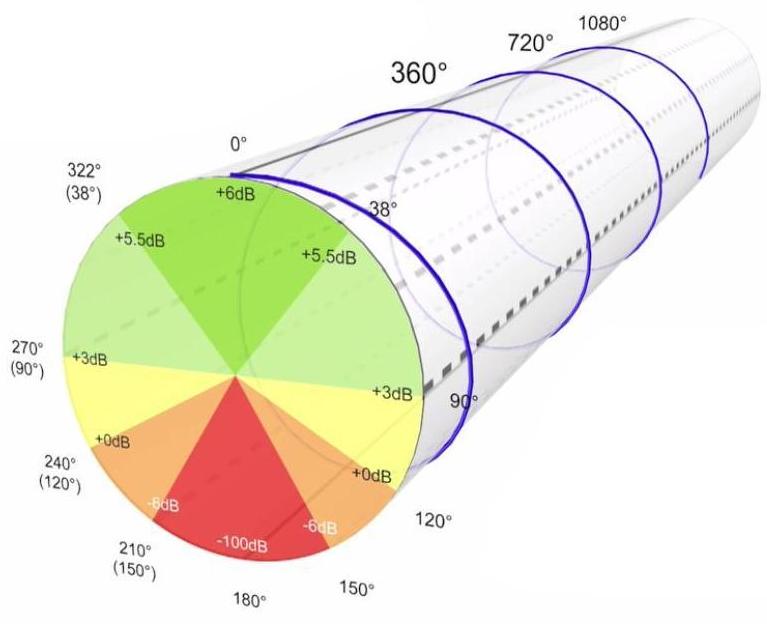
Un dernier exemple : 10 ms correspondent à une rotation de phase de 1440° à une fréquence de 400 Hz. La période d’une fréquence de 400 Hz est de 2,5 ms.
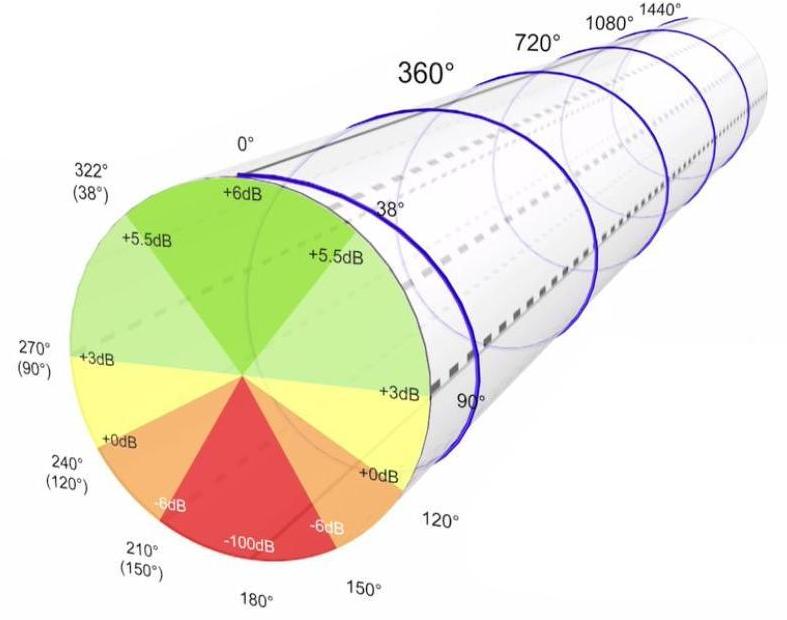
Afin de faciliter la lecture d’un tel graphique, nous allons le « dérouler » et le faire revenir en deux dimensions.
Nous voilà avec une visualisation en deux dimensions.
Attention !!! La progression des fréquences est ici linéaire !
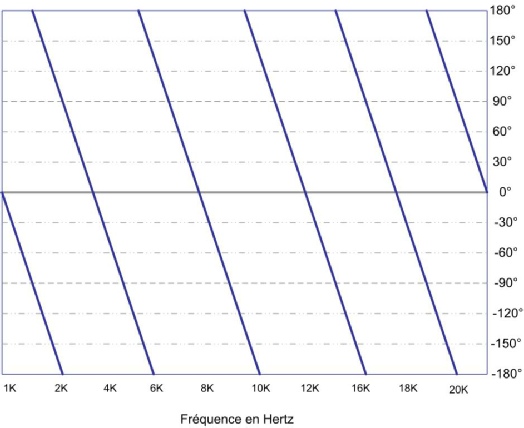
Afin de mieux visualiser la rotation de phase, des lignes verticales sont ajoutées au graphique. Ces lignes sont uniquement là pour nous aider à la compréhension du graphique ! Elles ne correspondent en rien à la réponse en phase.
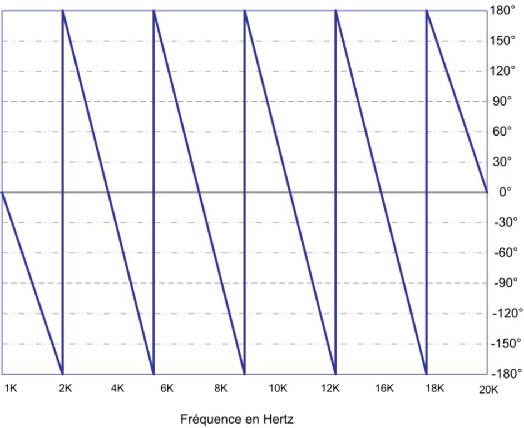
En progression logarithmique, cela nous donne ce graphique :
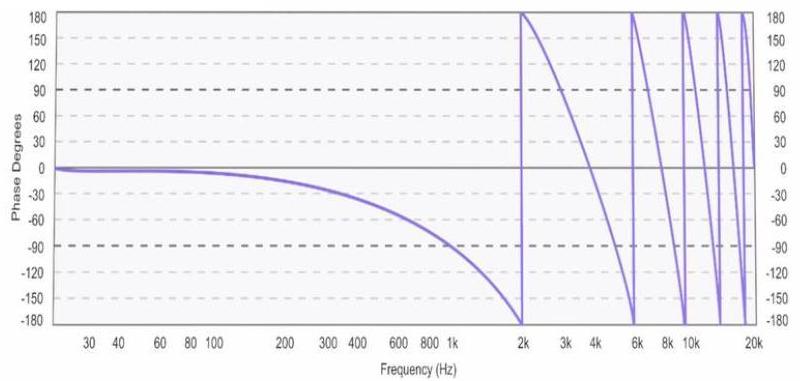
6. Visualisations via Smaart Live 6
Afin d’illustrer les graphiques ci-dessus, voyons quelques exemples de graphiques de réponse en phase via le logiciel Smaart Live 6.
Pour ce faire, nous avons utilisé une carte son Presonus Firebox et un processeur DBX 260.
Voici le principe de connexion :
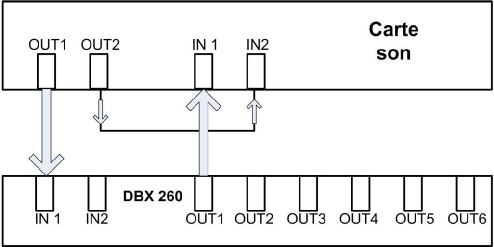
Un bruit rose est généré à partir de Smaart Live et envoyé vers les sorties OUT1 et OUT2 de la carte son.
La sortie 2 de la carte son est directement réinjectée dans l’entrée 2 de la carte son. Ce signal servira de référence pour Smaart Live.
La sortie 1 de la carte son est envoyée vers le DBX 260, ceci nous permettant d’appliquer un délai au signal pour le réinjecter dans l’entrée 1 de la carte son.
Entre le signal de référence et le signal traité par le DBX 260, Smaart nous donne un délai de 1,6 ms.
Ceci correspond au temps de traitement du signal audio par le DBX 260. Ce temps ne varie pas en fonction des différents processus enclenchés (EQ, filtres, délais,…).
Voici la réponse en phase du DBX 260 par rapport à notre référence :
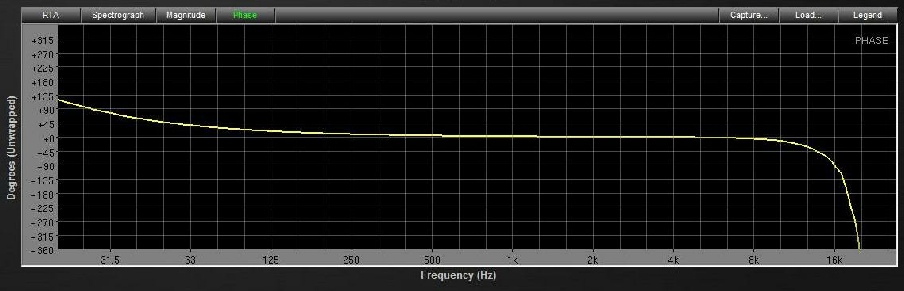
En ajoutant un délai de 2 ms à la sortie du DBX 260, cela nous donne le graphique suivant :
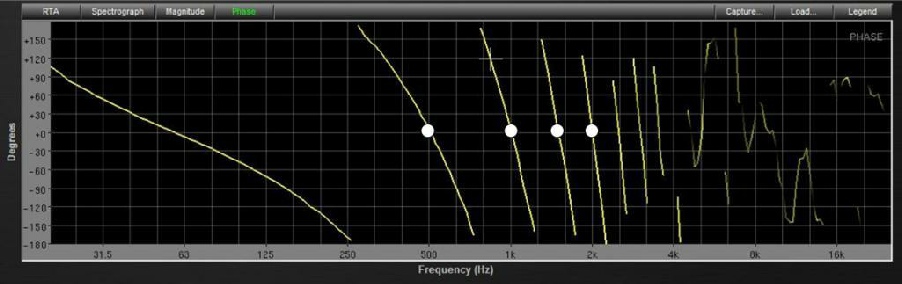
Le premier point blanc en partant de la gauche correspondent à une période pour une fréquence de 500 Hz soit 360°.
2 ms correspondent également à une demi- période d’où une rotation de 180° pour une fréquence de 250 Hz.
Ces 2 ms correspondent à une rotation de 720° (2 x 360°) pour une fréquence de 1000 Hz. Le deuxième point blanc sur le graphique. En effet, la période pour une fréquence de 1000 Hz est de 1 ms.
Le quatrième point blanc correspond à une rotation de 1440° (4 x 360°) pour une fréquence de 2 KHz. La période d’une fréquence de 2 KHz étant de 0,5 ms.
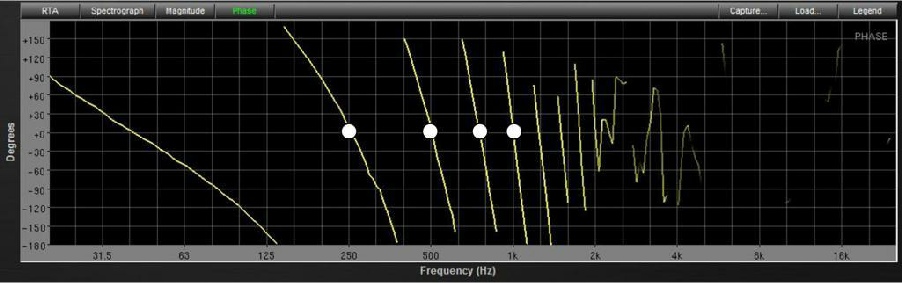
Ici, le délai appliqué est de 4 ms. Ces 4 ms correspondent à une période pour une fréquence de 250 Hz soit une rotation de 360°.
4 ms qui correspondent aussi à une rotation de 720° pour une fréquence de 500 Hz. Le deuxième point blanc sur le graphique.
Et à 1 KHz, cela correspond à une rotation de 1440° c’est-à-dire 4 fois la période.
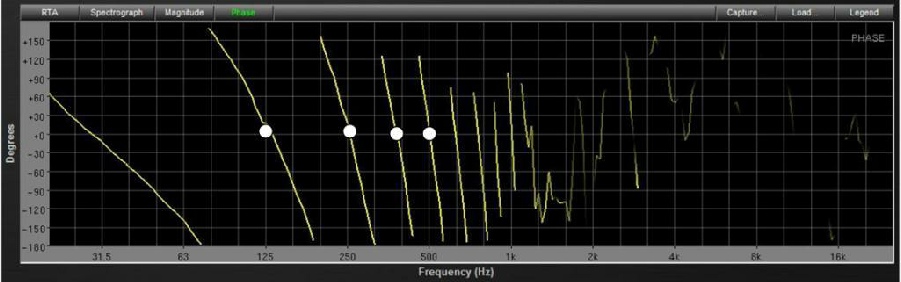
Le délai appliqué à la sortie du DBX 260 est de 8 ms.
Ces 8 ms correspondent à une période pour une fréquence de 125 Hz soit une avancée de 360°.
A 250 Hz, le deuxième point blanc, cela nous donne une avancée de 720°.
A 500 Hz, au quatrième point blanc, la rotation de phase est de 1440°.
Et ainsi de suite….
Courbe de réponse en phase : montante ou descendante ?
Petite expérience : Via Smaart Live, on génère un bruit rose envoyé vers un processeur.
La sortie 1 du processeur est envoyée vers l’entrée 1 de la carte son (normalement le canal de mesure).
La sortie 2 du processeur est envoyée vers l’entrée 2 de la carte son (normalement le canal de référence).
Un délai de 15 ms est appliqué à chaque sortie du processeur. L’analyse nous donne donc une réponse en phase parfaitement plate.
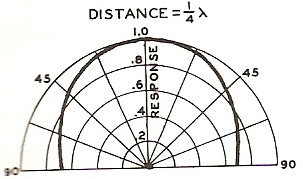
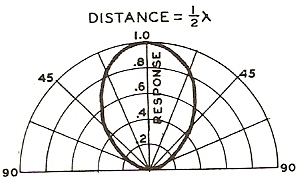
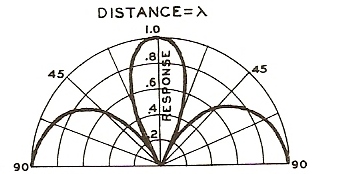
Les sources sont ici séparées de ¼ de la longueur d’onde, d’une ½ longueur d’onde et de la longueur d’onde. On remarque que plus l’espace entre les sources est grand, plus des lobes de directivités apparaissent.
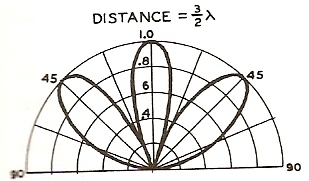
Ici, l’écart entre les sources est de 3/2 λ, 2 λ et 5/2 λ.
.jpg)
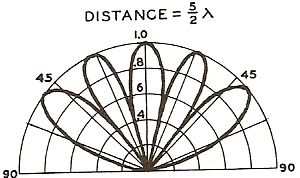
Voyons cela en pratique via plusieurs simulations réalisées via un logiciel informatique.
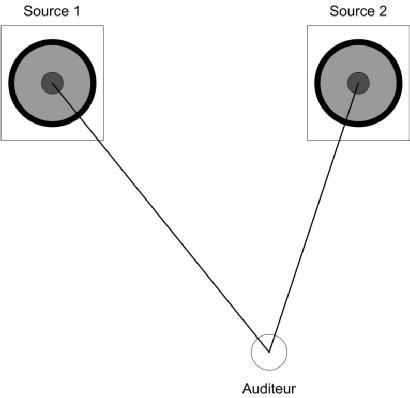
La situation est celle-ci :
Deux enceintes sont espacées l’une de l’autre d’une distance x. Distance correspondant dans nos exemples à ¼ λ, ½ λ, λ, 3/2 λ, 2 λ et 5/2 λ.
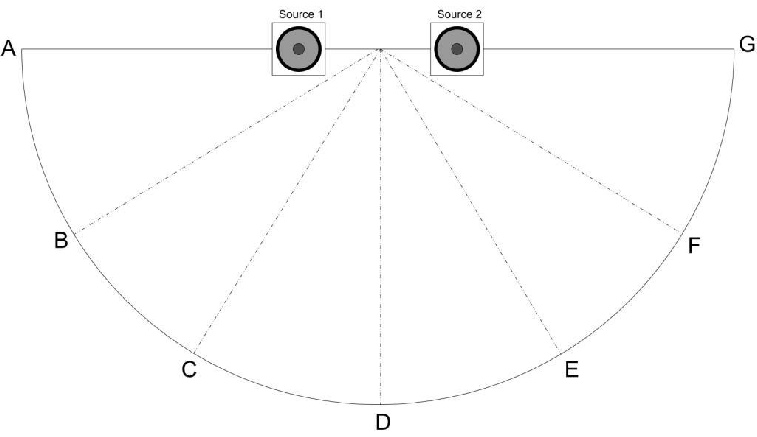
En utilisant la formule suivante, il va nous être possible de calculer le déphasage à différents endroits. On pourrait par exemple mesurer le déphasage aux positions A, B, C, D, E, F ou G.
Et pour cela, c’est-à-dire connaître la différence de phase à un endroit précis, il nous suffit d’utiliser la formule suivante :
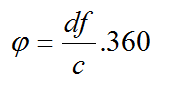
Où φ est le déphasage en degrés,
d la différence des distances entre les sources sonores et l’auditeur
C la vitesse du son
f la fréquence
Exemple :
L’auditeur se trouve parfaitement au milieu des deux enceintes, au sommet d’un triangle équilatéral.
La fréquence émise est de 100 Hz.
Le calcul est alors :
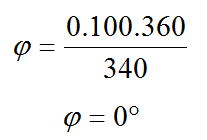
Il n’y a donc aucun déphasage. L’auditeur reçoit les deux sources en même temps.
Voici 6 exemples. Le calcul pour chaque cas correspond au déphasage dans l’axe horizontal. La fréquence utilisée est de 100 Hz.
1er cas : L’écart entre les sources est de 85 cm, soit le ¼ de la longueur d’onde.
Fréquence = 100Hz. Distance entre les sources = 0.85m
90° = 0.85m x 100Hz x 360° / 340m/s

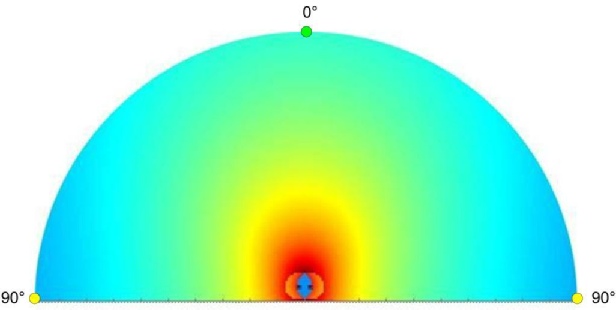
2ème cas : L’écart entre les sources est de ½ longueur d’onde.
Fréquence = 100Hz. Distance entre les sources = 1.7m
180° = 1.7m x 100Hz x 360° / 340m/s

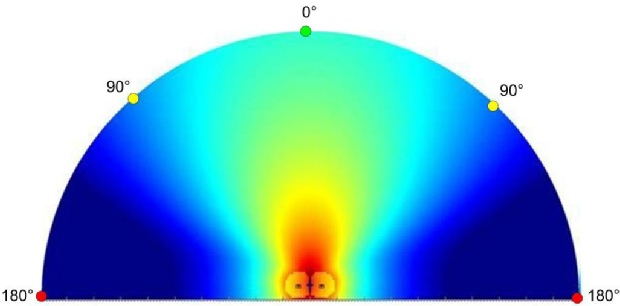
3ème cas : L’écart entre les sources est égal à la longueur d’onde
Fréquence = 100Hz. Distance entre les sources = 3.4m
(1 cycle) 360° = 3.4m x 100Hz x 360° / 340m/s

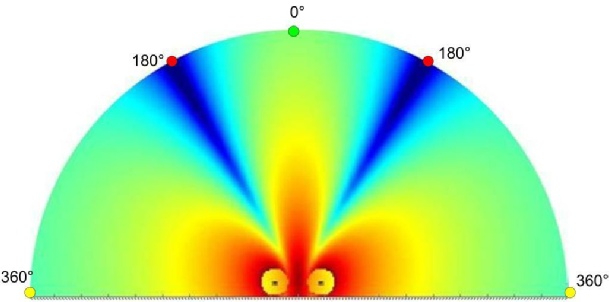
4ème cas : L’écart entre les deux sources est de 3/2 longueur d’onde
Fréquence = 100Hz. Distance entre les sources = 5.1m
(1 + ½ cycle) 540° = 5.1m x 100Hz x 360° / 340m/s

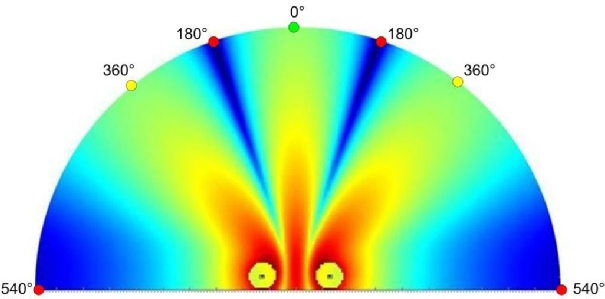
5ème cas : L’écart entre les sources est de 2 longueurs d’onde
Fréquence = 100Hz. Distance entre les sources = 6.8m
(2 cycles) 720° = 6.8m x 100Hz x 360° / 340m/s
.jpg)
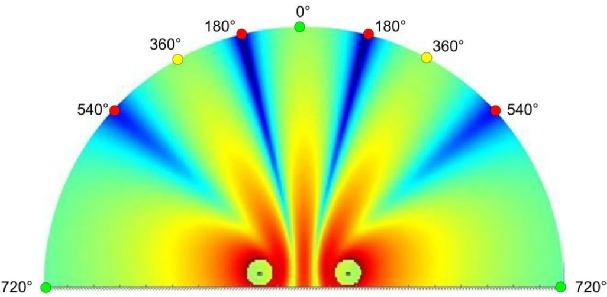
6ème cas : L’écart entre les sources est de 5/2 longueurs d’onde
Fréquence = 100Hz. Distance entre les sources = 8.5m
(2 + ½ cycles) 900° = 8.5m x 100Hz x 360° / 340m/s

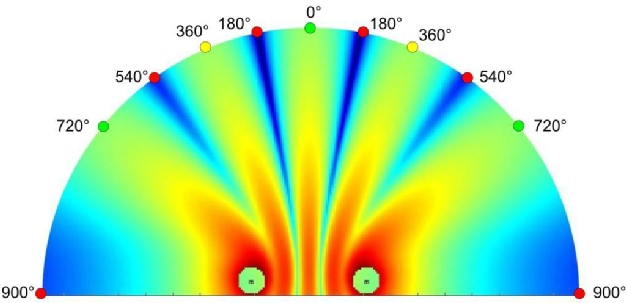
Repartons de ce graphique pour illustrer le phénomène de filtrage en peigne (Comb filter en anglais). Nos deux sources émettent simultanément le même signal.
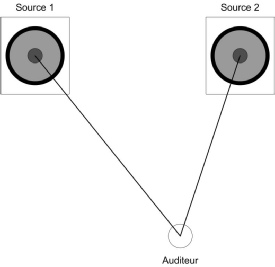
En supposant que l’auditeur se situe à une position non équidistante des deux sources, on constate que la pression sonore perçue à cet endroit va varier en fonction de la fréquence.
Il subira donc des maxima et minima et ceci selon la fréquence émise par les sources.
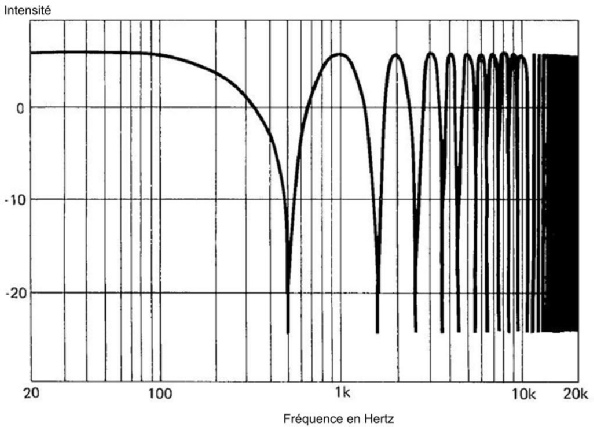
Exemple de réponse en fréquence suite au phénomène de filtrage en peigne.
Dans le cas de deux monopôles en phase (recevant le même signal au même instant), on pourra trouver :
Un premier minima à la fréquence f = c / 2d ou d correspond à la différence de distance entre les sources sonores et l’auditeur.
Un premier maxima à la fréquence 2 f
Une alternance de minima et de maxima séparés de f.
Quelques exemples :
Deux enceintes émettant le même signal sont placées de part et d’autre d’une scène. La distance qui sépare l’auditeur de la première enceinte est de 3 mètres. La distance qui sépare ce même auditeur à la deuxième enceinte est de 2 mètres. La distance d est donc de 1 mètre.
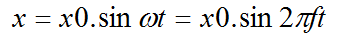
Exemple: une fréquence de 100 Hz.
Sa longueur d’onde est de 3,4 mètres, sa période est de 10 ms.
Le cercle trigonométrique tourne dans le sens inverse des aiguilles d’une montre.
L’expression mathématique de cette sinusoïde est la suivante :
D’un point de vue physique, on peut dire qu’une source est omnidirectionnelle si ses dimensions sont petites par rapport à la longueur d’onde du son émis.
Une petite source sera donc d’autant plus omnidirectionnelle que la fréquence émise est basse.
En effet, plus les longueurs d’onde seront grandes et plus la membrane d’un haut-parleur apparaîtra comme un point.
Cela nous permet d’établir les caractéristiques directives de deux petites sources distinctes vibrant en phase par rapport à la distance qui les sépare et la longueur d’onde.
Appliquons maintenant un délai supplémentaire de 3 ms à la sortie 1 du processeur.
La situation est donc la suivante :
Sortie 1 : 18 ms
Sortie 2 : 15 ms
Le canal 2 est donc en avance par rapport au canal 1.
Deuxième situation : revenons à la situation de base et appliquons un délai supplémentaire de 3 ms au canal 2.
La situation est donc la suivante :
Sortie 1 : 15 ms
Sortie 2 : 18 ms
Le canal 1 est donc en avance par rapport au canal 2.
On remarque que lorsque le canal 1 est en retard par rapport au canal 2, la courbe de réponse en phase est descendante.
A l’inverse, lorsque le canal 1 est en avance par rapport au canal 2, a courbe de réponse en phase est montante.
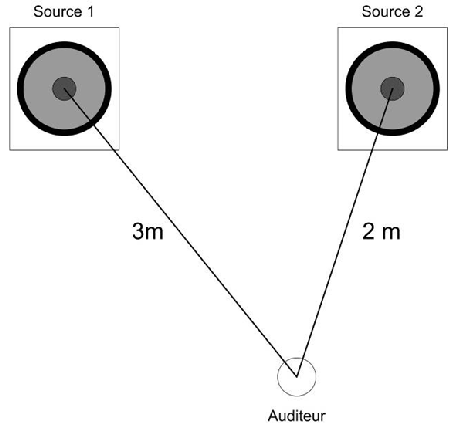
Le premier minima apparaîtra à une fréquence de f = c / 2d soit à 170 Hz. Un premier maxima à 2f soit 340 Hz.
En progression linéaire, le graphique du filtrage en peigne correspond à celui- ci :
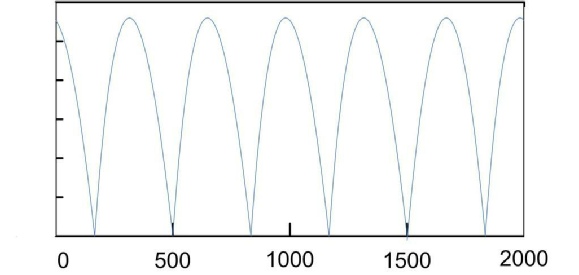
On pourrait également comparer ce schéma à une mesure d’analyse spectrale via un logiciel tel que Smaart Live, Spectrafoo,... Pour ce faire, le technicien place un micro à un endroit du lieu à sonoriser.
Si les deux côtés de la diffusion sont en marche, il y aura filtrage en peigne ! Il sera donc mieux de réaliser la mesure avec un seul côté en fonctionnement.
Cette fois, il n’y a qu’une seule source. On fait par contre intervenir les réflexions sonores suite à la présence d’obstacles. Là encore, il y aura filtrage en peigne.
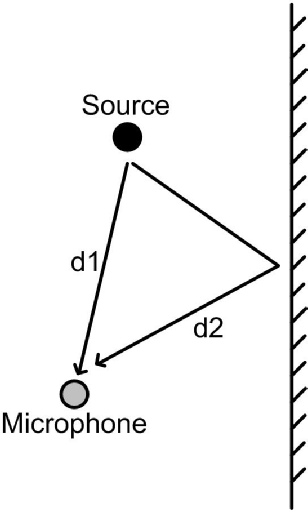
Deux microphones pour une même source sonore. Un mauvais placement pourra être la cause d’annulations à certaines fréquences.
…
Didier Pietquin 2008
Références, sources
- Audio, de Mario Rossi. Presses polytechniques et universitaires romandes, 2007
- Acoustical Engineering, de Harry F. Olson. Professional Audio Journals Inc, 1991
- Sono, de Michael Ebner. Publitronic, 2002
- http://www.meyersound.com
- http://www.techniquesduson.com

| Moteur de recherche |
| Plan du site |
| Blog |
| Son |
| Eclairage |
| Electricité |
| Câblage et connectique |
| Bien débuter |
| Acoustique |
| Line Array - Ligne source |
| Impédance - HP |
| Décibels |
| DI Box |
| Adaptation d'impédance |
| Symétrique - Asymétrique |
| Lignes 100 volts |
| Consoles |
| Acoustique fondamentale |
| Timbre |
| Phase: Première partie |
| Directivité des basses fréquences |
| End fire |
| End Fire 2 |
| Sources sonores - propagation |
| WST |
| Circuits auxiliaires |
| INSERTS |
| Groupes |
| Bouchon DMX |
| Câbles multipaires électriques |
| Electricité - Notions élémentaires |
| Tableaux électriques |
| L'électricité pour nos spectacles |
| Multimètres - Utilisation |
| Indices de protection (IP) |
| Branchements |
| Relier les enceintes |
| Les types de câbles |
| Câbles électriques |
| Réaliser ses adaptateurs |
| Connecter un clavier |
| Série et parallèle |