


La directivité des basses fréquences
Comment créer un sub cardioïde, comment gérer la directivité des basses fréquences ? C’est ce que nous allons tenter d’éclaircir dans ce sujet.
Rapide rappel sur le filtrage en peigne
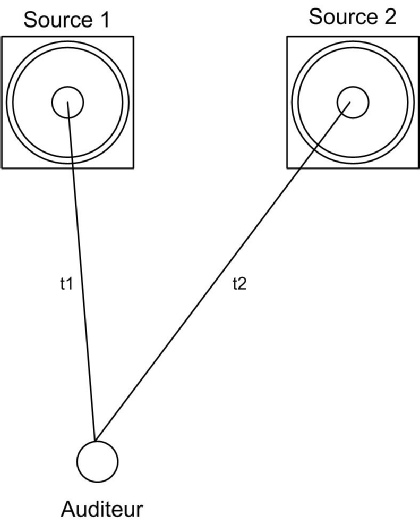
Prenons trois situations classiques et courantes. Dans la première, un auditeur va recevoir avec une différence de temps les sources 1 et 2 qui émettent le même signal.
Dans la deuxième, la différence de temps est cette fois provoquée par le fait que le son rencontre des obstacles (murs, sol,…).
Dans la troisième, deux microphones captent le son provenant d’un même instrument.
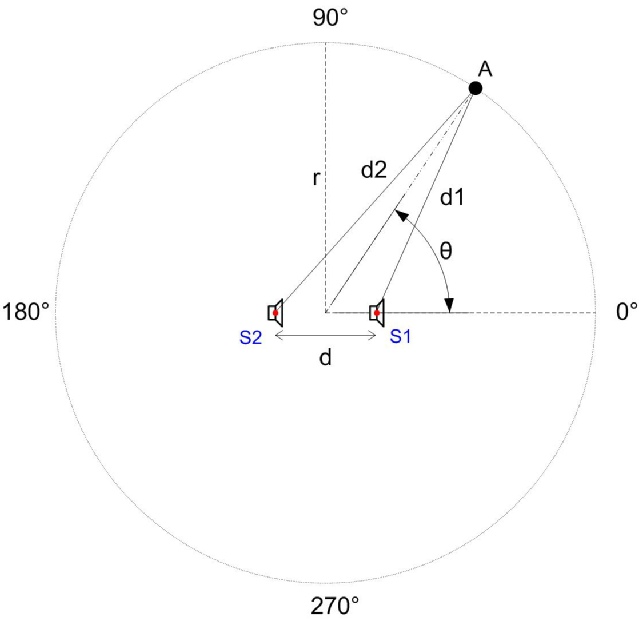
Nous avons choisi arbitrairement de prendre pour nos calculs un rayon de 10 mètres.
La fréquence qui sera utilisée est de 100 Hz.
La célérité utilisée est de 340m/s (vitesse de propagation du son dans l’air).
|
Fréquence |
Longueur d’onde: λ=C/f |
Période: T=1/f |
|
100 Hz |
3,4 m |
0.01 s soit 10 ms |
Premier cas, décalage spatial entre deux sources
Nos deux sources sonores identiques sont espacées d’une distance d. Notre auditeur est donc distant de d1 par rapport à la source S1 et de d2 par rapport à la source S2.
Ces distances d1 et d2 seront donc variables par rapport à la place de notre auditeur (angle et distance) et de la distance d qui sépare nos deux sources.
Notre but est calculer la différence de distance (∆d) entre d1 et d2, afin de traduire cette valeur en degrés, correspondant à un déphasage φ, déphasage dépendant de la fréquence et de la distance séparant les centres acoustiques de ces sources.
Ce qui nous permettra de connaître l’incidence de la place de l’auditeur par rapport à nos deux sources sonores.
Pour cela, nous utiliserons la formule suivante :
Et pour connaître les distances d1 et d2, nous utiliserons les formules suivantes :
Et donc de calculer la différence entre les deux :
Pour illustrer ces formules, prenons quelques exemples chiffrés.
Et nous choisirons arbitrairement les valeurs suivantes : Le rayon du cercle est de 10 mètres, la distance séparant les deux sources est de 1,2 m. L’angle est de 30°.
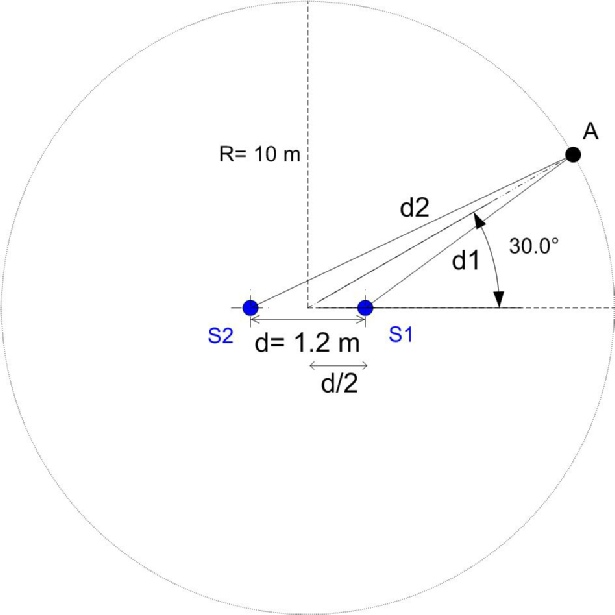
Ce qui nous donne :
d1 =
d1= 9,49 mètres
et
d2 =
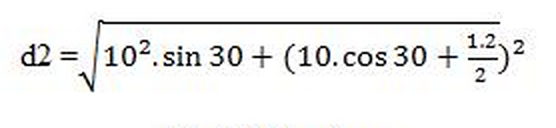
d2= 10,52 mètres
Il est donc facile de calculer la différence Δd en effectuant d2 – d1 ou en utilisant la formule suivante, pour ceux qui sont accros aux maths !
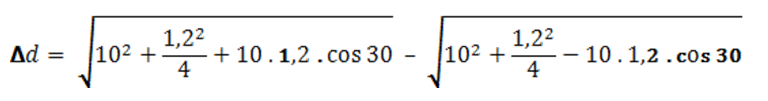
∆d = 1,03 m
Et pour connaître le déphasage :
L’auditeur reçoit donc le signal des deux sources sonores avec un déphasage de 110°.
Mêmes calculs mais pour un angle de 90° cette fois.
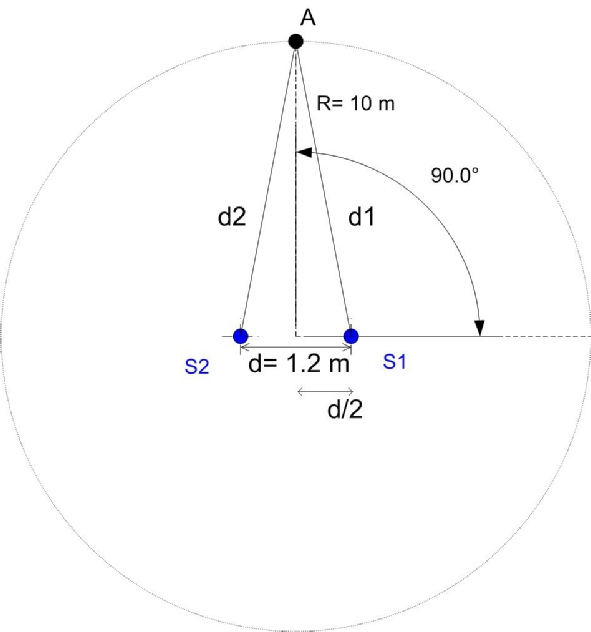
d1= 10,02 mètres
d2= 10,02 mètres
∆d= 0 m
Soit φ = = 0°
Les deux sources sont parfaitement en phase puisque l’auditeur se trouve à égale distance des sources S1 et S2.
Dernier exemple, en gardant les mêmes valeurs mais en prenant un angle de 180°.
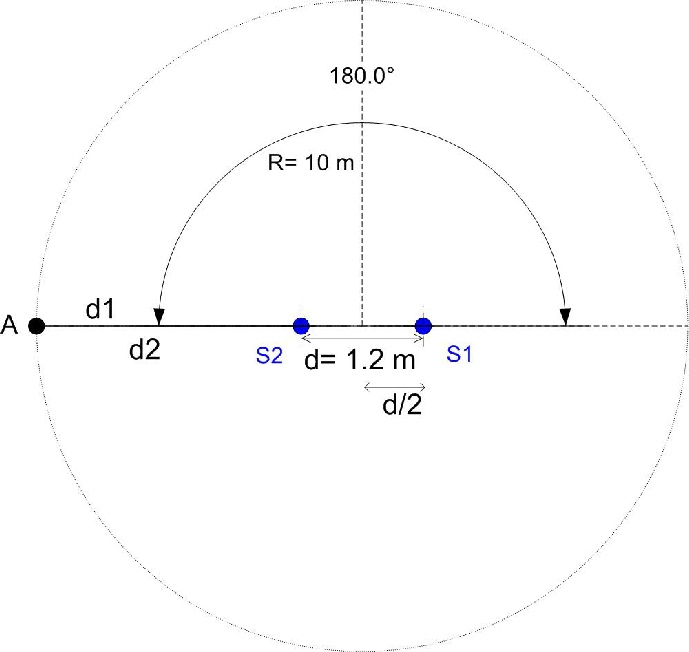
Il est facile de constater que ∆d sera de 1,2 m dans ce cas- ci. Mais vérifions tout de même cette réponse :
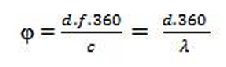
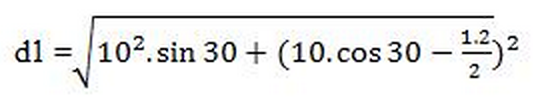

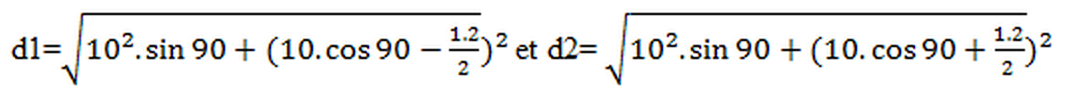
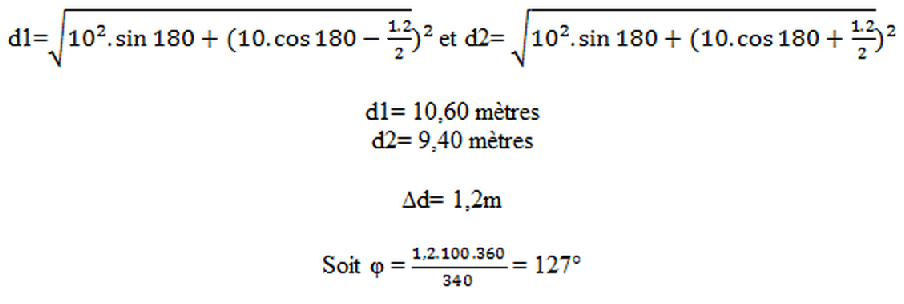
Petit résumé des valeurs trouvées:
Pour rappel, il s’agit des valeurs trouvées avec une fréquence de 100 Hz! Toute autre fréquence entraînera des valeurs différentes.
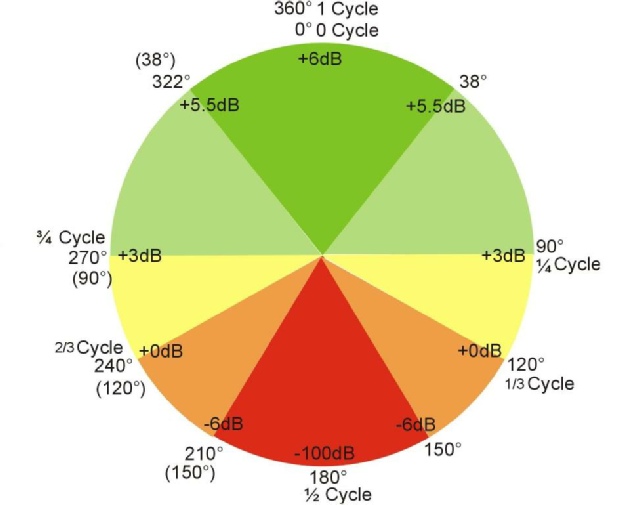
Et sous le tableau, le cercle nous permettant de connaître la valeur en dB par rapport au déphasage.
|
Angle de l’auditeur par rapport à l’axe principal |
Déphasage résultant (+/-) |
|
0° |
127° |
|
45° |
89° |
|
90° |
0° |
|
135° |
- 89° |
|
180° |
- 127° |
|
225° |
- 89° |
|
270° |
0° |
|
315° |
89° |
|
360° |
127° |
On peut également effectuer une vérification en réalisant une simulation via Mapp Online de Meyer. Les sources sont des subs 500HP, l’écart est bien de 1,2 m entre-elles et la fréquence de simulation est de 100 Hz.
Voici ce que cela donne :
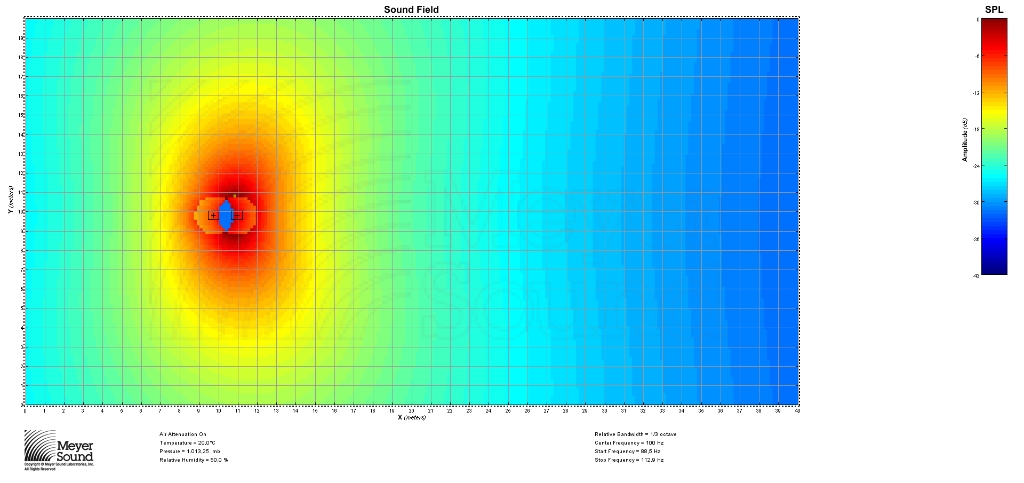
Les exemples ci-dessus ont été réalisés avec une distance d de 1,2 m et une fréquence de 100 Hz.
Et si l’on prend cette fois une distance d équivalente à la longueur d’onde, soit 3,4 m, voici ce que cela donne :
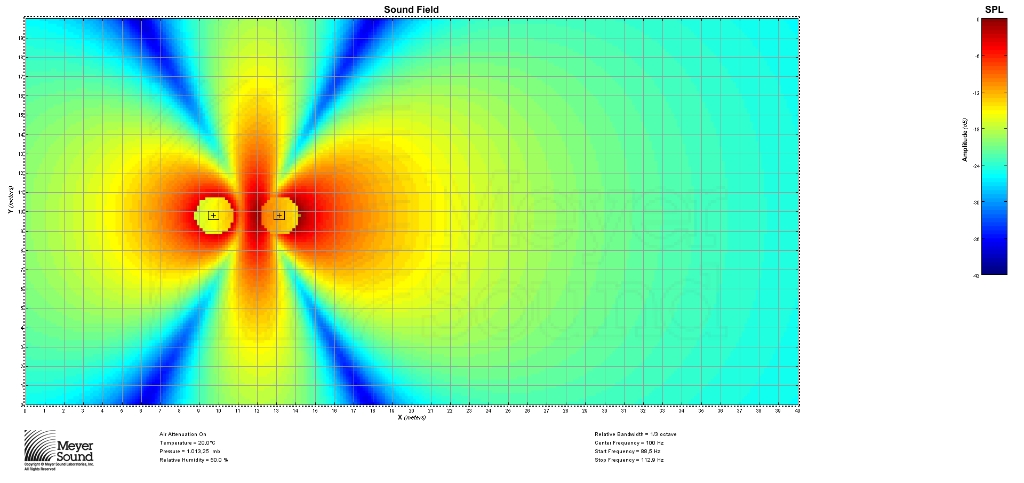
En multipliant les simulations et comme nous l’avons vu dans notre article sur la phase, on remarque que plus l’espace entre les sources est grand, plus des lobes de directivités apparaissent.
Deuxième cas : retard temporel
Ici, la situation est différente.
Si on applique un délai à une enceinte, on la « déplace » virtuellement. Connaissant la célérité du son dans l’air (340m/s dans nos exemples), il est très simple de faire correspondre un délai en seconde à une distance en mètre. (On ne s’occupe pas de la fréquence pour l’instant.)
D = T x 340 ou T = D/ 340
Par exemple, on applique un délai de 10 ms soit 0,01 s à une enceinte.
D= T x 340 soit D= 0,01 x 340 = 3,4 mètres.
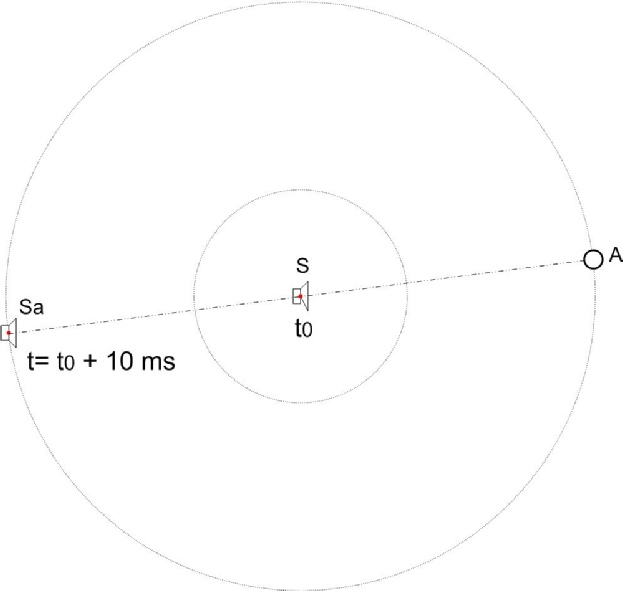
La source est donc éloignée virtuellement de 3,4 m par rapport à l’auditeur.
Et le fait qu’elle s’éloigne plutôt que de se rapprocher est facile à comprendre. Prenez deux voitures de courses sur un circuit. Plus l’une prendra de l’avance, plus la distance entre-elles sera importante et donc le temps également.
La source sonore retardée S2 se déplacera donc virtuellement (pour se trouver en S2b) en fonction de la place de l’auditeur, alors que la source S1 restera au même endroit.
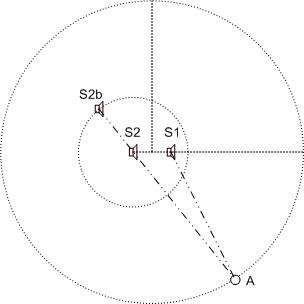
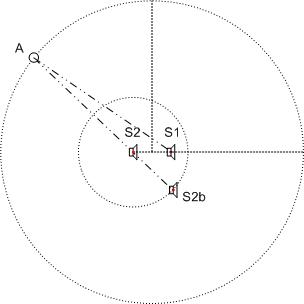
Reprenons nos deux sources. Nous prendrons comme décalage spatial d (= 1,2 m) entre S1 et S2, la source S2 est retardée avec un temps t.
En gardant notre fréquence de 100 Hz, commençons avec l’angle de 30°.
Le délai appliqué à S2 est de 3,5 ms, correspondant à la distance d (ou D= T x 340 soit D= 0,0035 x 340 = 1,2 mètres).
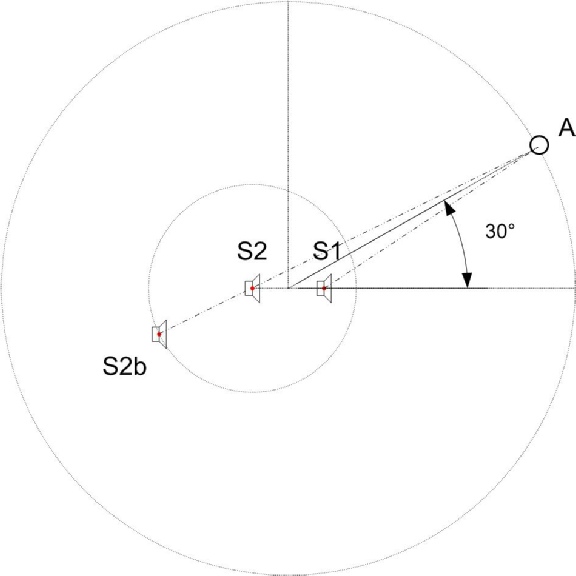
La distance que nous avions trouvée en d1 était de 9,49 m.
La distance trouvée en d2 était de 10,52 m auxquels nous rajoutons la distance « virtuelle » de 1,2 m soit un total de 11,72 m.
La différence est donc de 2,23 m.
Pour une fréquence de 100 Hz, cela correspond à un déphasage de 237°.
Pour rappel, φ= (d .f.360)/c = (d .360)/λ
Pour un angle de 0°, la distance d1 est de 9,40 m. La distance d2 est de 10,60 m + 1,2 m soit 11,80 m. La différence est donc de 2,4m.
Cela correspond à un déphasage de 254°.
Pour un angle de 90°, la distance d1 est de 10,02 m. d2 est de 10,02 m + 1,2 soit 11,22 m. La différence est de 1,2 m. Cela correspond à un déphasage de 180°.
Pour un angle de 180°, la distance d1 est de 10,60m. d2 vaut 9,40 m+ 1,2 soit 10,60 m soit une différence nulle. Cela correspond à un déphasage de 0°.
Pour un angle de 270°, la distance d1 est de 10,02 m. d2 est de 10,02 m + 1,2 soit 11,22 m. La différence est de 1,2 m. Cela correspond à un déphasage de 180°.
Donc, reprenons nos différentes valeurs :
Pour un angle de 0°, le déphasage est de 254°.
Pour un angle de 90°, le déphasage est de 180°.
Pour un angle de 180°, le déphasage est de 0°.
Pour un angle de 270°, le déphasage est de 180°.
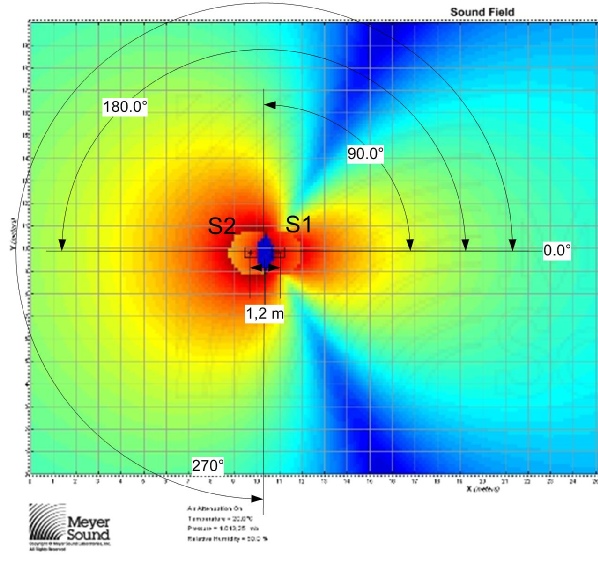
La simulation ci-dessus nous confirme nos calculs. Elle est réalisée avec deux subs 500 HP, séparés de 1,2m, rayonnants dans l’axe 0°. Un délai de 3,5 ms est appliqué au sub S2.
Applications pour contrôler la directivité des basses fréquences
Premier cas : Utilisation d’un dipôle
Un dipôle est constitué de deux sources sonores identiques séparées par une distance d, distance beaucoup plus petite que la longueur d’onde.
Elles sont de polarité inversée.
En utilisant le principe du dipôle, voyons comment créer une directivité cardioïde.
Pour ne pas changer les bonnes habitudes, nos deux sources sont espacées d’une distance d et sont cette fois de polarité inversée.
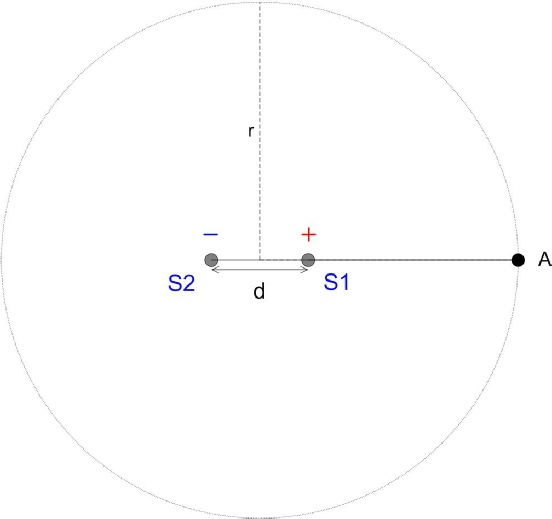
Gardons toujours notre fréquence de 100 Hz dont la longueur d’onde est de 3,4 mètres.
Nous réaliserons trois simulations avec les données suivantes :

A noter que le délai appliqué correspond à la distance d (d = T x 340 ou T = d/ 340)
Voici les résultats :
Première simulation :
Deuxième simulation :
Troisième simulation :
Ok, c’est donc la troisième simulation qui est la plus intéressante pour nous. La distance d est égale au quart de la longueur d’onde pour une fréquence de 100 Hz soit 85 cm et le retard appliqué au sub arrière est de 2,5 ms. Sans oublier l’inversion de phase.
Décalage spatial, retard temporel
Les prochains paragraphes de cet article sont destinés à comprendre la différence entre un décalage spatial entre deux sources sonores identiques et un retard temporel appliqué à une des deux sources.
Nous réaliserons ici différents calculs et simulations à l’aide du logiciel Mapp Online de Meyer Sound.
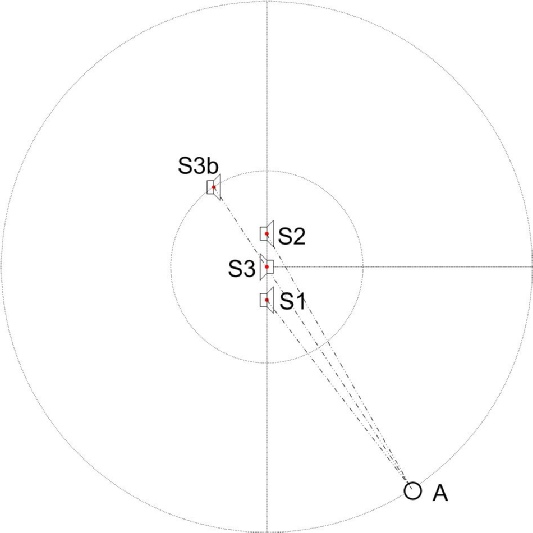
Et pour ce faire, voici le schéma qui nous servira de base pour nos différents exemples.
Il s’agit de deux sources sonores identiques (S1 et S2) espacées d’une distance d, l’axe 0° étant l’axe de diffusion. Le centre du cercle est le point milieu de l’axe entre S1 et S2.
r correspond au rayon du cercle et un auditeur se trouve au point A.
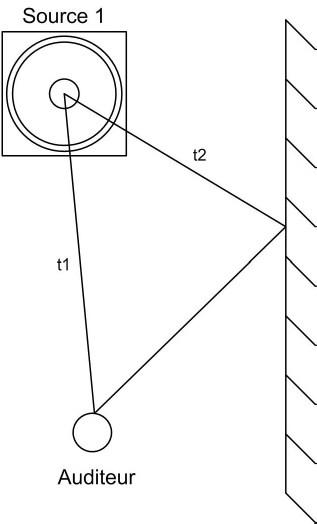
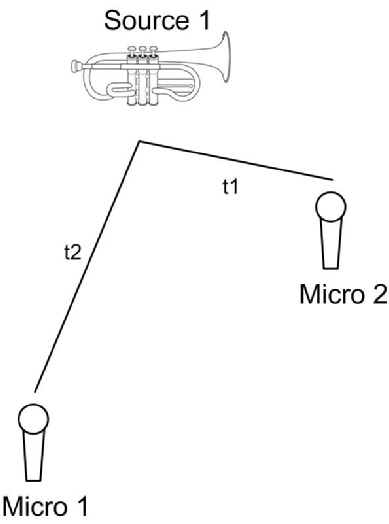
Dans tous les cas, ce décalage spatial (et donc temporel puisque le son se propage à une vitesse de 340m/s) va introduire un déphasage.
Ce déphasage va dépendre de la différence de distance et de la fréquence émise.
La première annulation aura lieu à
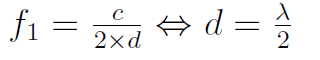
La fréquence centrale de la deuxième annulation aura lieu à
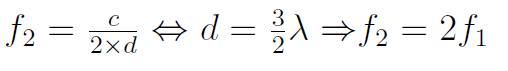
Par exemple, dans notre premier cas, imaginons que t1 soit égal à 3 mètres, t2 à 2 mètres. La différence vaut donc 1 mètre.
La première annulation aura lieu à 340/2x1 soit 170 Hz.
On aurait encore pu parler en temps plutôt qu’en distance.
Connaissant la vitesse du son, cette différence de 1 mètre équivaut à 1/340 soit environ 3 ms.
On sait que la première annulation aura lieu à d= λ/2.
3 ms étant la période d’une fréquence de 340 Hz, on peut en déduire que la première annulation aura lieu à 170 Hz (demi longueur d’onde ou demi période).
Il faut également tenir compte que pour les hautes fréquences, ces phénomènes d’annulation sont extrêmement proches et du coup négligeables.
De même que la différence de niveau provoquée par une distance importante entre les sources fait que le phénomène devient également négligeable.
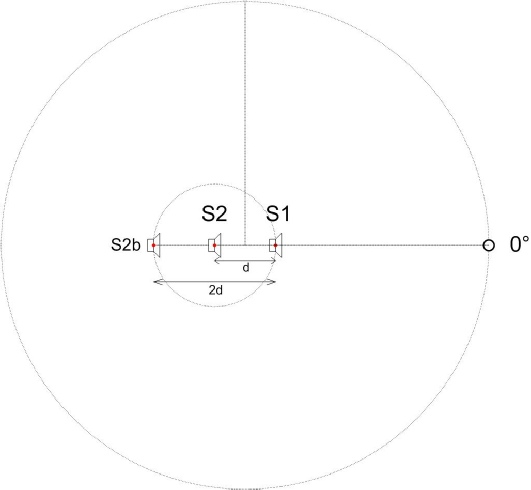
Plaçons-nous à l’axe 0°.
La situation est donc la suivante : Le sub S2 est éloigné physiquement du sub S1 de 85 cm dans notre cas. Il est également éloigné temporellement de 2,5 ms, il se retrouve donc virtuellement à l’emplacement S2b.
Puisque d correspond à λ/4, 2 x d correspond à λ/2. Comme les deux sources sont en opposition de phase, la sommation est parfaite.
Plaçons- nous à l’axe des 180°.
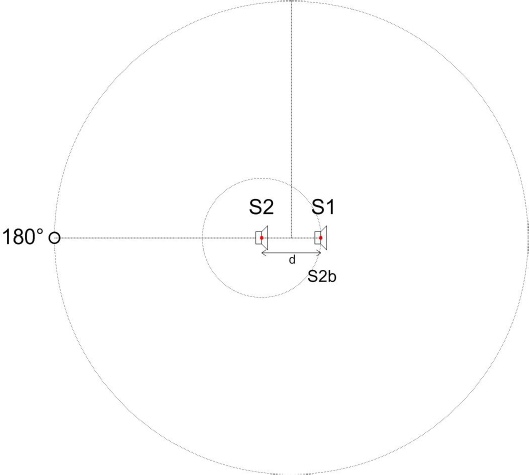
Dans ce cas- ci, l’image virtuelle de S2 est maintenant confondue avec S1.
Les deux sources étant en opposition de phase, il y a annulation.
Ce qu’on l’on peut vérifier sur notre troisième simulation ci-dessus.
Et en augmentant la fréquence ? (On ne change ni le délai ni l’emplacement des subs)
Pour rappel, la fréquence utilisée est de 100 Hz. Sa longueur d’onde est de 3,4 mètres.
Selon le schéma ci- dessous, le rapport D/ λ dans notre cas vaut 0,5.
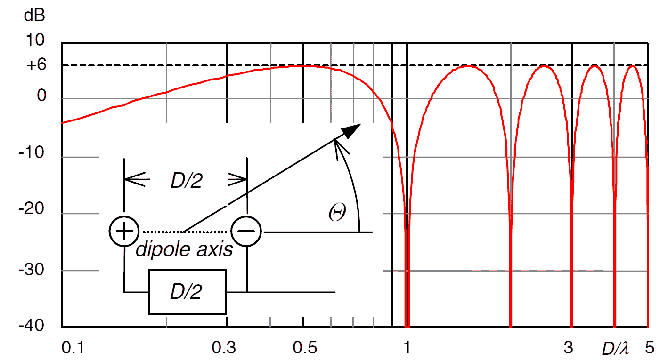
En effet, D/2= 85 cm. D vaut donc 1,7 m.
Le rapport D/ λ (1,7/3,4) = 0,5.
Lorsque la fréquence augmente, ce rapport augmente. Si l’on prend la fréquence de 200 Hz, sa longueur d’onde est de C/f soit 340/200 = 1,7m.
Le rapport D/ λ va évoluer : 1,7/1,7 soit 1.
En prenant 300 Hz (longueur d’onde 1,13 m), le rapport D/ λ vaut 1,7/1,13 soit 1,5.
En théorie, cela donne ça :
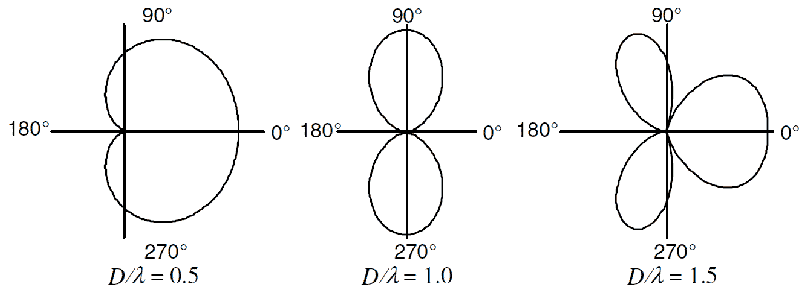
En pratique, voici 3 simulations réalisées avec deux subs 700-HP de Meyer (Subs espacés de 85 cm, délai de 2,5 ms et inversion de phase pour le sub arrière) :
A 100 Hz
A 200 Hz
A 315 Hz
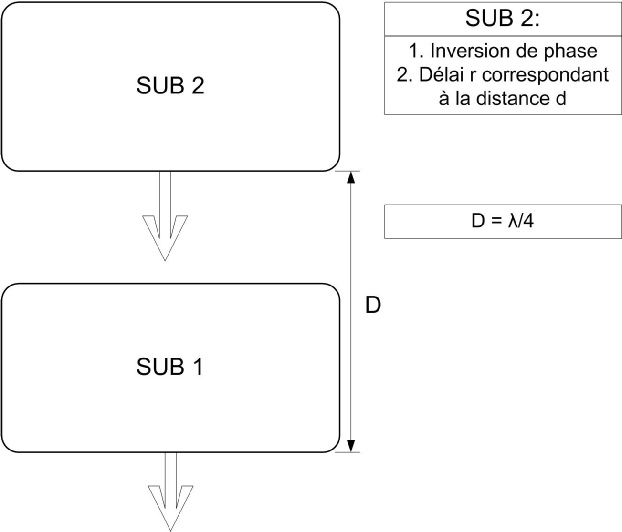
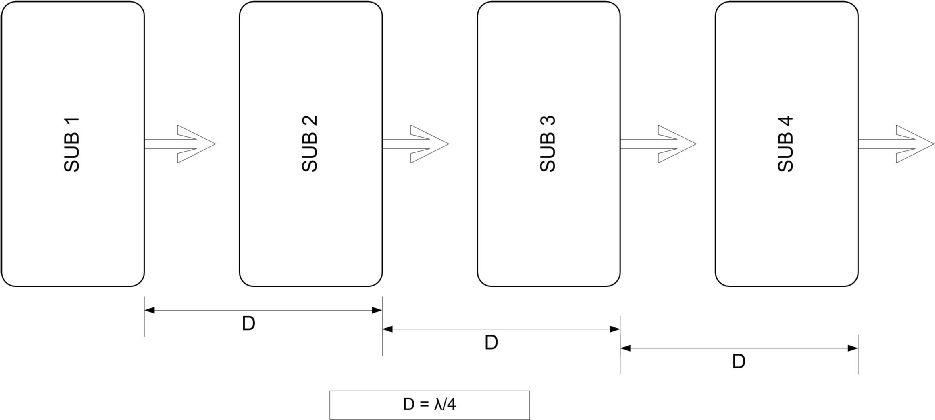
Chaque sub est espacé d’une distance D, correspondant au quart de la longueur d’onde de la fréquence choisie.
Un délai est appliqué au sub 2, correspondant à la distance D.
Ce délai est doublé pour le sub 3 et est triplé pour le sub 4.
Exemple : Nos subs sont espacés d’un mètre, le délai appliqué au deuxième sub est de 2,94 ms, 5,88 ms au sub 3 et 8,82 ms au sub 4.
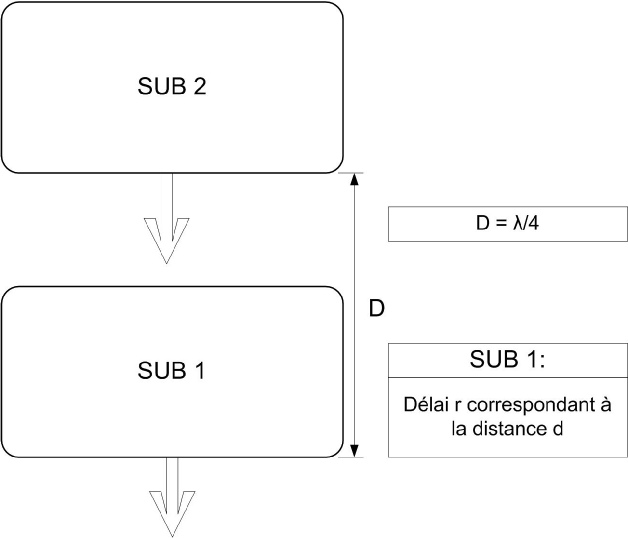
Exemple : On souhaite obtenir un montage cardioïde à 63Hz.
λ= C/F soit 5,4m
λ/4 = 1,35 m
Le retard à appliquer au sub S1 est donc de T=d/340 soit 4 ms.
On peut également prolonger notre montage en rajoutant des subs.
Le principe théorique est le suivant :
Exemple : On souhaite obtenir un montage cardioïde à 63Hz.
λ= C/F soit 5,4m
λ/4 = 1,35 m
Le retard à appliquer au sub S2 est donc de T=d/340 soit 4 ms.
Dans ce cas-ci, plus d’inversion de phase pour le sub arrière.
Et le délai n’est non plus appliqué au sub arrière mais au sub avant.
Je vous invite à visiter le site de Bob Mc Carthy pour d’autres explications très complètes sur le mode End Fire!
Didier Pietquin 2013
Références, sources
- Audio, de Mario Rossi. Presses polytechniques et universitaires romandes, 2007
- Acoustical Engineering, de Harry F. Olson. Professional Audio Journals Inc, 1991
- Article d’Alain Pouillon-Guibert du Sonomag 341 - Décembre 2008.
- http://www.meyersound.com
- http://www.techniquesduson.com
Et n’hésitez pas à tester vos propres configurations! Voici un programme gratuit pour effectuer un tas de simulations: DDT disponible sur le site http://www.danleysoundlabs.com/
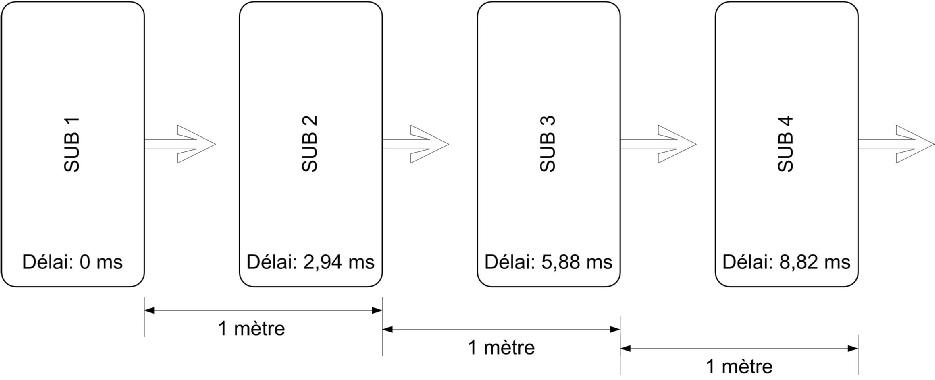
Image: Alain Pouillon- Guibert
Image: Alain Pouillon- Guibert
Troisième cas, troisième possibilité:
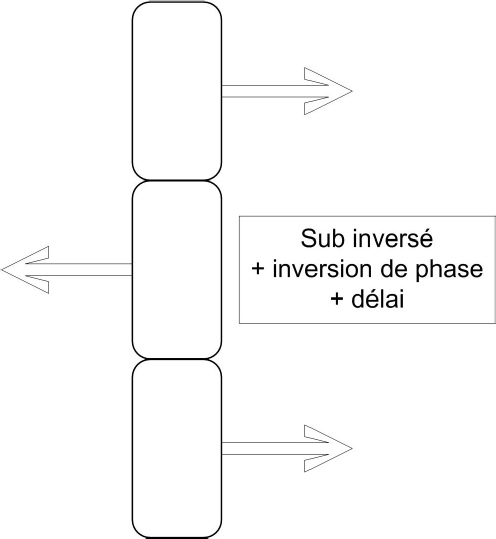
Cela revient à :
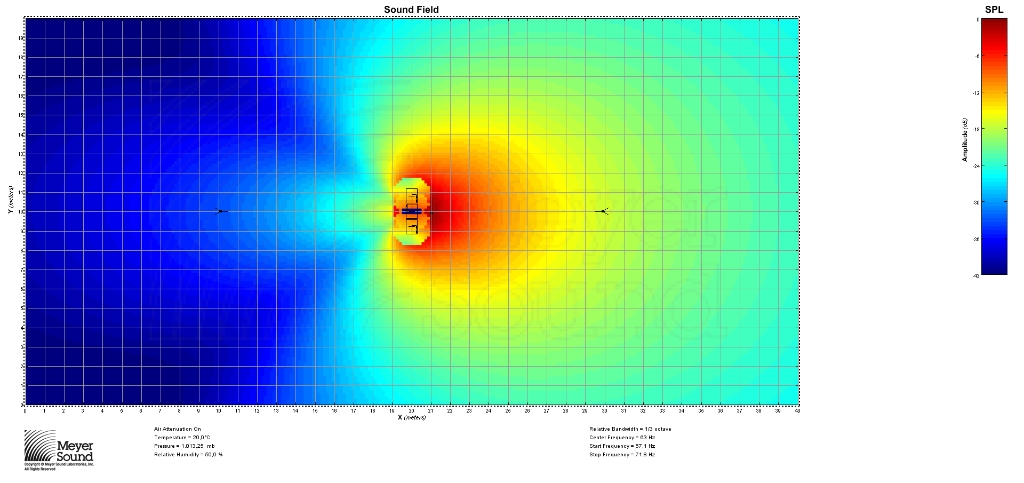
Voici une simulation réalisée avec 3 subs 650P.
Un délai de 3,32 ms est appliqué au sub central, de même qu’une inversion de phase.

| Moteur de recherche |
| Plan du site |
| Blog |
| Son |
| Eclairage |
| Electricité |
| Câblage et connectique |
| Bien débuter |
| Acoustique |
| Line Array - Ligne source |
| Impédance - HP |
| Décibels |
| DI Box |
| Adaptation d'impédance |
| Symétrique - Asymétrique |
| Lignes 100 volts |
| Consoles |
| Acoustique fondamentale |
| Timbre |
| Phase: Première partie |
| Directivité des basses fréquences |
| End fire |
| End Fire 2 |
| Sources sonores - propagation |
| WST |
| Circuits auxiliaires |
| INSERTS |
| Groupes |
| Bouchon DMX |
| Câbles multipaires électriques |
| Electricité - Notions élémentaires |
| Tableaux électriques |
| L'électricité pour nos spectacles |
| Multimètres - Utilisation |
| Indices de protection (IP) |
| Branchements |
| Relier les enceintes |
| Les types de câbles |
| Câbles électriques |
| Réaliser ses adaptateurs |
| Connecter un clavier |
| Série et parallèle |